Коан о панельных данных
R
Загрузим необходимые библиотеки.
library(plm) # Работа с панельными данными
library(lmtest) # Оценка регрессий и ковариационных матриц параметров
library(skimr) # Красивый summary
library(car) # Линейные модели
library(gplots) # Графики гетерогенности
library(rio) # Чтение данных
library(tidyverse) # Обработка данных
Загрузим данные и преобразуем нужные переменные в факторные. В данном разделе все визуализации будут построены на подмножестве данных из шести индивидов и нескольких временных точек. Это позволит не перегружать графики. Все модели будут оценены на большом массиве данных.
panel = import('../data/09_small.csv')
panel = mutate(panel, black = factor(black), id = factor(id))
Изобразим наши панельные данные на диаграмме рассеяния. Дополнительно установим параметр сглаживания, чтобы получить кривые временных рядов. Ненежным элементам графика поставим в соответствие значение “FALSE”
ggplot(data = panel, aes(y = lwage, x = year, color = id)) + geom_smooth(aes(group = id), se = FALSE) +
geom_point(aes(color = id)) + ylab("Log(wage)") + xlab("Year")
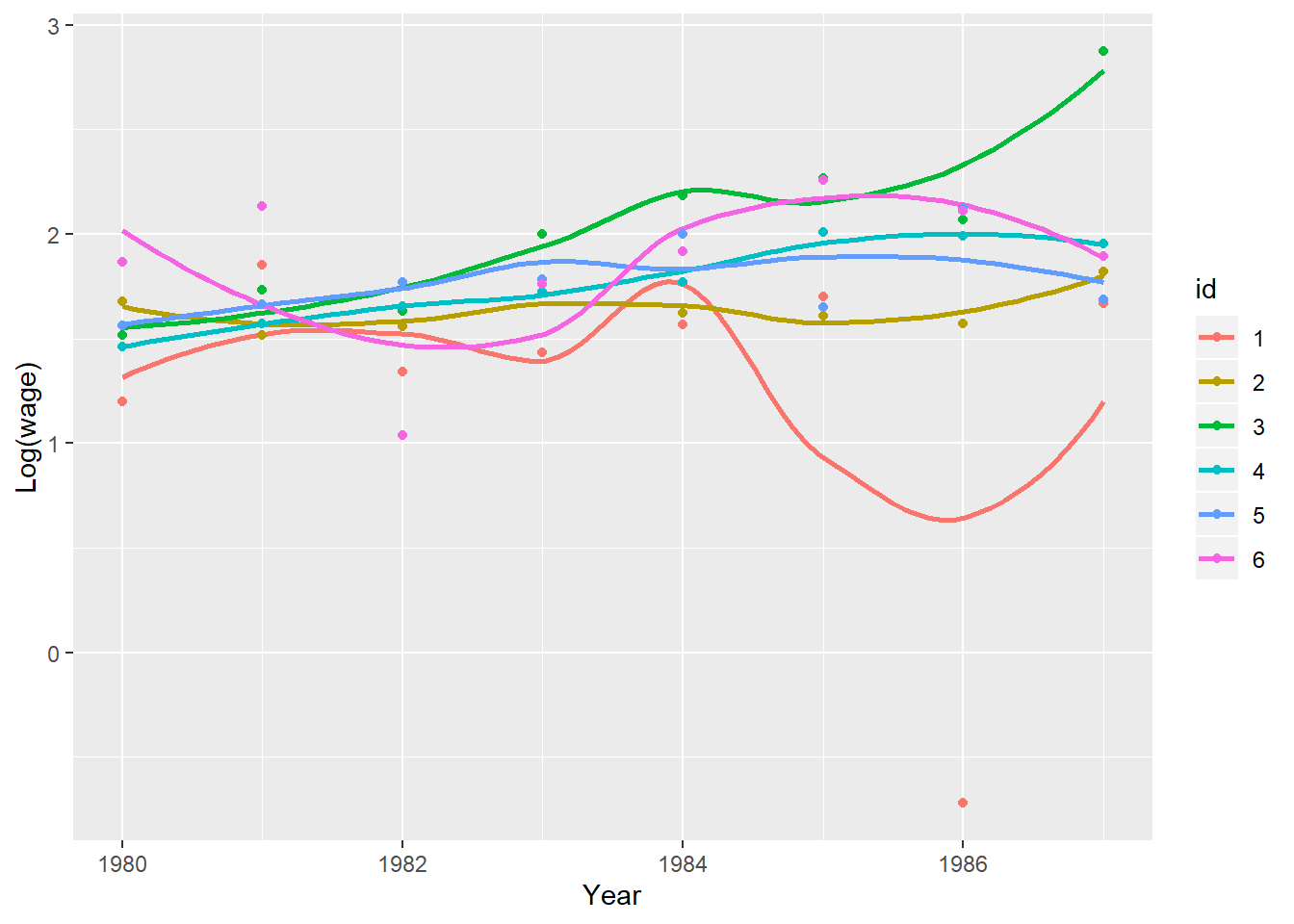
Можно сгруппировать данные по различным признакам. Например, в зависимости от расы индивидов.
ggplot(data = panel) + geom_point(aes(x = year, y = lwage)) + geom_smooth(aes(x = year, y = lwage), se = FALSE) + facet_wrap(~black) + ylab("Log(wage)") + xlab("Year")
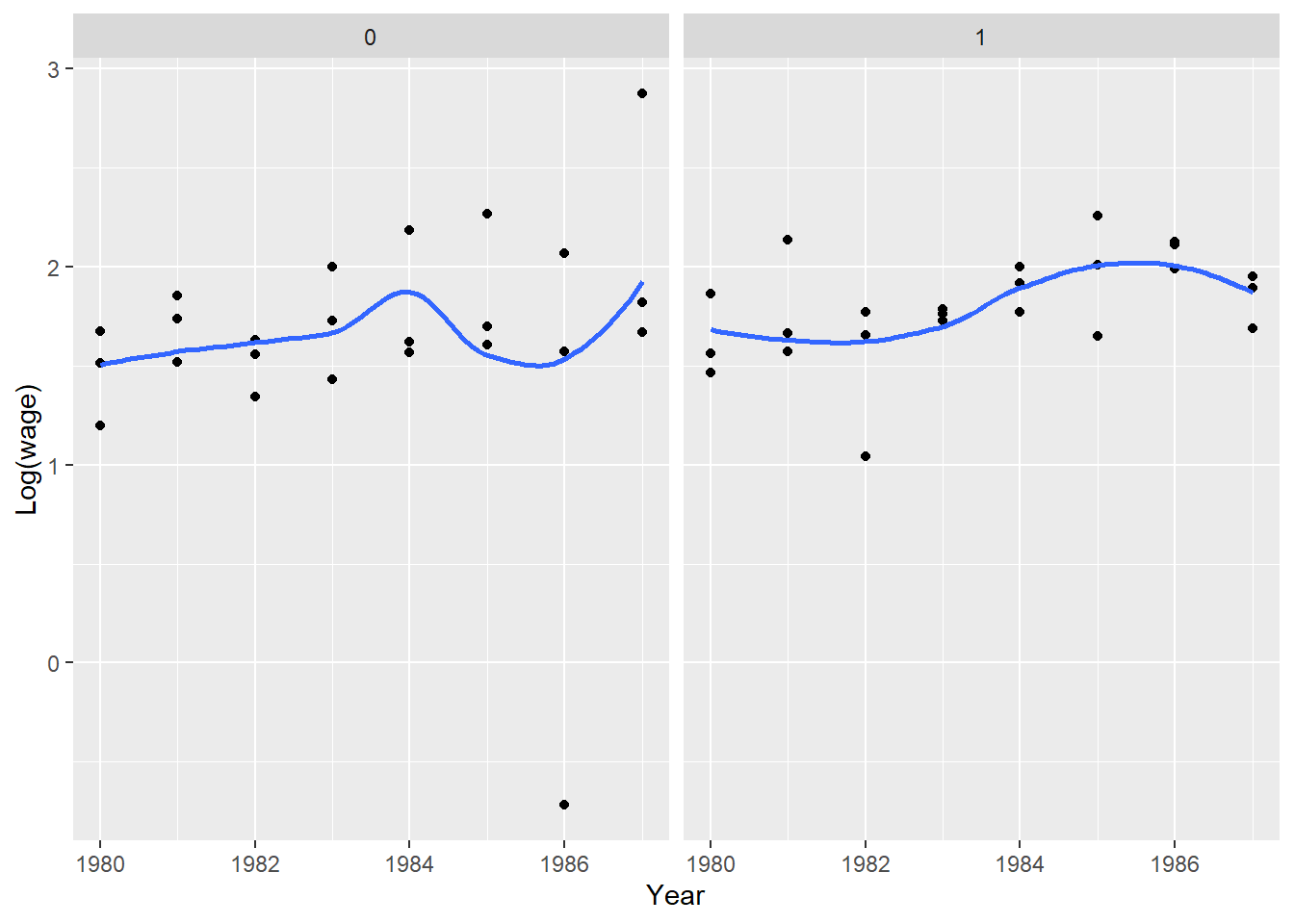
Импортируем основной датасет.
Panel = import('../data/09_large.csv')
Визуализируем гетерогенный эффект. Можно визуализировать по годам или по индивидам. Здесь уже можно использовать полный датасет. Так как доверительные интервалы с интервалом в год не пересекаются, можно увидеть явную гетерогенность.
plotmeans(lwage ~ year, main = "Heterogeineity across years", data=Panel)
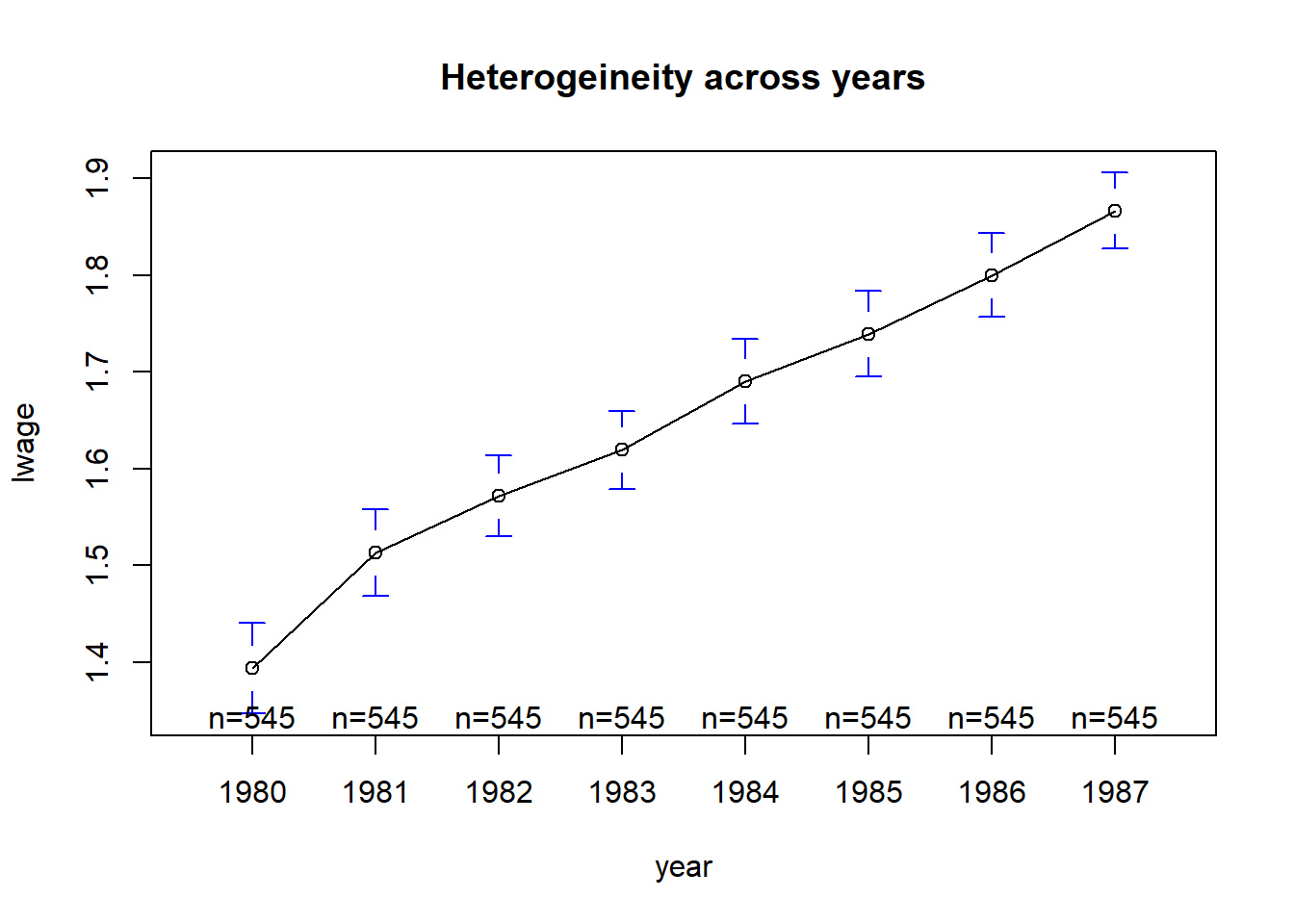
Модель панельных данных будет выглядеть следующим образом:
\[\begin{equation}
y_{i t}=\alpha+x_{i t}^{\prime} \beta+z_{i}^{\prime} \gamma+c_{i}+u_{i t}
\end{equation}\]
где \(\alpha\) — константа, \(c_{i}\) — индивидуальные эффекты индивидов, а \(z_i\) — независимые от времени переменные. Следовательно, матрица \(X\) — матрица зависимых от времени регрессов, \(Z\) — матрица независимых от времени регрессоров. Дополнительно обозначим как \(l_n\) вектор из единиц.
Оценим простую модель с фиксированными эффектами через within-оценку. Вычитая \(\overline{y}_{i}=1 / T \sum_{t} y_{i t}\) из исходной модели, получим within-модель:
\[\begin{equation}
\ddot{y}_{i t}=\ddot{x}_{i t}^{\prime} \beta+\ddot{u}_{i t}
\end{equation}\]
где \(\ddot{y}_{i t}=y_{i t}-\overline{y}_{i}, \ddot{x}_{i t k}=x_{i t k}-\overline{x}_{i k}\) and \(\ddot{u}_{i t}=u_{i t}-\overline{u}_{i}\). Следует заметить, что константа \(\alpha\), индивидуальные эффекты \(c_i\) и инвариантные ко времени регрессоры \(z_i\) исчезают из модели.
\[\begin{equation}
\widehat{\beta}_{F E}=\left(\ddot{X}^{\prime} \ddot{X}\right)^{-1} \ddot{X}^{\prime} \ddot{y}
\end{equation}\]
ffe = plm(lwage ~ hours, model = "within", data = Panel)
summary(ffe)
Oneway (individual) effect Within Model
Call:
plm(formula = lwage ~ hours, data = Panel, model = "within")
Balanced Panel: n = 545, T = 8, N = 4360
Residuals:
Min. 1st Qu. Median 3rd Qu. Max.
-4.116091 -0.136963 0.015755 0.182507 1.555059
Coefficients:
Estimate Std. Error t-value Pr(>|t|)
hours -5.5854e-07 1.4013e-05 -0.0399 0.9682
Total Sum of Squares: 572.05
Residual Sum of Squares: 572.05
R-Squared: 4.1656e-07
Adj. R-Squared: -0.14289
F-statistic: 0.00158875 on 1 and 3814 DF, p-value: 0.96821
Проверим значимость коэффициентов, используя ковариационную матрицу ошибок Хубера – Уайта.
coeftest(ffe, vcov=vcovHC(ffe, cluster="group"))
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
hours -5.5854e-07 2.5051e-05 -0.0223 0.9822
Оценим модель со случайными эффектами, используя достижимый обобщённый МНК (FGLS).
\[\begin{equation}
\left(\begin{array}{c}{\widehat{\alpha}_{R E}} \\ {\widehat{\beta}_{R E}} \\ {\widehat{\gamma}_{R E}}\end{array}\right)=\left(W^{\prime} \widehat{\Omega}_{v}^{-1} W\right)^{-1} W^{\prime} \widehat{\Omega}_{v}^{-1} y
\end{equation}\]
где
\(W=\left[\iota_{N T} X Z\right] \text { и } \iota_{N T} \text { это вектор из единиц размерности } N T \times 1\)
fre = plm(lwage ~ hours, model = "random", data = Panel)
summary(fre)
Oneway (individual) effect Random Effect Model
(Swamy-Arora's transformation)
Call:
plm(formula = lwage ~ hours, data = Panel, model = "random")
Balanced Panel: n = 545, T = 8, N = 4360
Effects:
var std.dev share
idiosyncratic 0.1500 0.3873 0.528
individual 0.1341 0.3663 0.472
theta: 0.6498
Residuals:
Min. 1st Qu. Median 3rd Qu. Max.
-4.506028 -0.164365 0.028671 0.218928 1.605623
Coefficients:
Estimate Std. Error z-value Pr(>|z|)
(Intercept) 1.6459e+00 3.3705e-02 48.8332 <2e-16 ***
hours 1.4611e-06 1.3348e-05 0.1095 0.9128
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Total Sum of Squares: 653.53
Residual Sum of Squares: 653.53
R-Squared: 2.7494e-06
Adj. R-Squared: -0.00022671
Chisq: 0.0119818 on 1 DF, p-value: 0.91284
Проверим значимость коэффициентов, используя ковариационную матрицу ошибок Хубера – Уайта.
coeftest(fre, vcov = vcovHC(ffe, cluster = "group"))
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
hours 1.4611e-06 2.5051e-05 0.0583 0.9535
Проведём тест Хаусмана.
phtest(ffe, fre)
Hausman Test
data: lwage ~ hours
chisq = 0.22438, df = 1, p-value = 0.6357
alternative hypothesis: one model is inconsistent
Построим FD-оценку.
\[\begin{equation}
\dot{y}_{i t}=\dot{x}_{i t}^{\prime} \beta+\dot{u}_{i t}
\end{equation}\]
\(\dot{y}_{i t}=y_{i t}-y_{i, t-1}, \dot{x}_{i t}=x_{i t}-x_{i, t-1}\) и \(\dot{u}_{i t}=u_{i t}-u_{i, t-1}\)
fd = plm(lwage ~ hours - 1, model = "fd", data = Panel)
summary(fd)
Oneway (individual) effect First-Difference Model
Call:
plm(formula = lwage ~ hours - 1, data = Panel, model = "fd")
Balanced Panel: n = 545, T = 8, N = 4360
Observations used in estimation: 3815
Residuals:
Min. 1st Qu. Median Mean 3rd Qu. Max.
-4.4590 -0.0585 0.0554 0.0793 0.1935 4.7557
Coefficients:
Estimate Std. Error t-value Pr(>|t|)
hours -2.0303e-04 1.4585e-05 -13.92 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Total Sum of Squares: 751.19
Residual Sum of Squares: 731.45
R-Squared: 0.058688
Adj. R-Squared: 0.058688
F-statistic: 102.938 on 1 and 3814 DF, p-value: < 2.22e-16
Построим МНК-оценку с дамми-переменными по каждому индивиду (LSDV). Видим, что численно её результаты идентичны withih-регрессии, как и должно быть.
lsdv = lm(lwage ~ hours + factor(id) - 1, data = Panel)
summary(lsdv)
Call:
lm(formula = lwage ~ hours + factor(id) - 1, data = Panel)
Residuals:
Min 1Q Median 3Q Max
-4.1161 -0.1370 0.0158 0.1825 1.5551
Coefficients:
Estimate Std. Error t value Pr(>|t|)
hours -5.585e-07 1.401e-05 -0.040 0.968208
factor(id)1 1.257e+00 1.425e-01 8.825 < 2e-16 ***
factor(id)2 1.639e+00 1.413e-01 11.597 < 2e-16 ***
factor(id)3 2.036e+00 1.408e-01 14.455 < 2e-16 ***
factor(id)4 1.775e+00 1.404e-01 12.639 < 2e-16 ***
factor(id)5 2.056e+00 1.401e-01 14.680 < 2e-16 ***
factor(id)6 1.435e+00 1.424e-01 10.076 < 2e-16 ***
factor(id)7 1.996e+00 1.418e-01 14.077 < 2e-16 ***
factor(id)8 1.065e+00 1.434e-01 7.426 1.37e-13 ***
factor(id)9 1.474e+00 1.398e-01 10.537 < 2e-16 ***
factor(id)10 1.395e+00 1.394e-01 10.005 < 2e-16 ***
factor(id)11 1.385e+00 1.378e-01 10.052 < 2e-16 ***
factor(id)12 2.193e+00 1.396e-01 15.711 < 2e-16 ***
factor(id)13 1.840e+00 1.404e-01 13.103 < 2e-16 ***
factor(id)14 2.060e+00 1.413e-01 14.581 < 2e-16 ***
factor(id)15 2.455e+00 1.405e-01 17.468 < 2e-16 ***
factor(id)16 1.675e+00 1.400e-01 11.963 < 2e-16 ***
factor(id)17 1.697e+00 1.411e-01 12.031 < 2e-16 ***
factor(id)18 2.033e+00 1.398e-01 14.544 < 2e-16 ***
factor(id)19 2.214e+00 1.425e-01 15.533 < 2e-16 ***
factor(id)20 1.525e+00 1.400e-01 10.896 < 2e-16 ***
factor(id)21 1.726e+00 1.401e-01 12.321 < 2e-16 ***
factor(id)22 1.769e+00 1.400e-01 12.635 < 2e-16 ***
factor(id)23 2.077e+00 1.408e-01 14.754 < 2e-16 ***
factor(id)24 2.368e+00 1.400e-01 16.919 < 2e-16 ***
factor(id)25 1.311e+00 1.443e-01 9.085 < 2e-16 ***
factor(id)26 1.700e+00 1.399e-01 12.153 < 2e-16 ***
factor(id)27 2.284e+00 1.409e-01 16.214 < 2e-16 ***
factor(id)28 1.411e+00 1.411e-01 10.000 < 2e-16 ***
factor(id)29 7.640e-01 1.412e-01 5.409 6.71e-08 ***
factor(id)30 1.950e+00 1.403e-01 13.895 < 2e-16 ***
factor(id)31 1.670e+00 1.402e-01 11.917 < 2e-16 ***
factor(id)32 1.928e+00 1.407e-01 13.709 < 2e-16 ***
factor(id)33 2.362e+00 1.396e-01 16.918 < 2e-16 ***
factor(id)34 1.098e+00 1.409e-01 7.791 8.49e-15 ***
factor(id)35 2.103e+00 1.402e-01 14.995 < 2e-16 ***
factor(id)36 1.657e+00 1.402e-01 11.816 < 2e-16 ***
factor(id)37 1.664e+00 1.416e-01 11.753 < 2e-16 ***
factor(id)38 1.694e+00 1.406e-01 12.045 < 2e-16 ***
factor(id)39 2.063e+00 1.416e-01 14.576 < 2e-16 ***
factor(id)40 1.657e+00 1.400e-01 11.833 < 2e-16 ***
factor(id)41 5.381e-01 1.386e-01 3.883 0.000105 ***
factor(id)42 7.392e-01 1.390e-01 5.319 1.10e-07 ***
factor(id)43 1.713e+00 1.388e-01 12.345 < 2e-16 ***
factor(id)44 1.782e+00 1.408e-01 12.660 < 2e-16 ***
factor(id)45 1.989e+00 1.399e-01 14.215 < 2e-16 ***
factor(id)46 1.763e+00 1.413e-01 12.476 < 2e-16 ***
factor(id)47 1.128e+00 1.393e-01 8.095 7.63e-16 ***
factor(id)48 2.019e+00 1.416e-01 14.260 < 2e-16 ***
factor(id)49 8.453e-01 1.383e-01 6.112 1.08e-09 ***
factor(id)50 1.874e+00 1.409e-01 13.301 < 2e-16 ***
factor(id)51 1.759e+00 1.391e-01 12.644 < 2e-16 ***
factor(id)52 1.487e+00 1.397e-01 10.648 < 2e-16 ***
factor(id)53 2.212e+00 1.413e-01 15.658 < 2e-16 ***
factor(id)54 1.182e+00 1.391e-01 8.494 < 2e-16 ***
factor(id)55 2.022e+00 1.403e-01 14.411 < 2e-16 ***
factor(id)56 1.301e+00 1.390e-01 9.354 < 2e-16 ***
factor(id)57 1.353e+00 1.420e-01 9.525 < 2e-16 ***
factor(id)58 2.352e+00 1.406e-01 16.729 < 2e-16 ***
factor(id)59 2.146e+00 1.398e-01 15.346 < 2e-16 ***
factor(id)60 1.435e+00 1.400e-01 10.249 < 2e-16 ***
factor(id)61 1.250e+00 1.436e-01 8.703 < 2e-16 ***
factor(id)62 2.068e+00 1.402e-01 14.756 < 2e-16 ***
factor(id)63 1.305e+00 1.410e-01 9.257 < 2e-16 ***
factor(id)64 1.965e+00 1.404e-01 13.994 < 2e-16 ***
factor(id)65 1.374e+00 1.395e-01 9.852 < 2e-16 ***
factor(id)66 1.379e+00 1.421e-01 9.704 < 2e-16 ***
factor(id)67 1.181e+00 1.415e-01 8.346 < 2e-16 ***
factor(id)68 1.779e+00 1.401e-01 12.702 < 2e-16 ***
factor(id)69 1.157e+00 1.439e-01 8.040 1.19e-15 ***
factor(id)70 2.089e+00 1.387e-01 15.058 < 2e-16 ***
factor(id)71 2.081e+00 1.403e-01 14.829 < 2e-16 ***
factor(id)72 1.780e+00 1.400e-01 12.714 < 2e-16 ***
factor(id)73 1.927e+00 1.405e-01 13.716 < 2e-16 ***
factor(id)74 1.546e+00 1.395e-01 11.084 < 2e-16 ***
factor(id)75 1.874e+00 1.402e-01 13.369 < 2e-16 ***
factor(id)76 1.319e+00 1.397e-01 9.444 < 2e-16 ***
factor(id)77 1.935e+00 1.400e-01 13.819 < 2e-16 ***
factor(id)78 1.469e+00 1.420e-01 10.343 < 2e-16 ***
factor(id)79 1.782e+00 1.393e-01 12.792 < 2e-16 ***
factor(id)80 1.677e+00 1.484e-01 11.304 < 2e-16 ***
factor(id)81 2.016e+00 1.399e-01 14.405 < 2e-16 ***
factor(id)82 1.291e+00 1.407e-01 9.175 < 2e-16 ***
factor(id)83 1.650e+00 1.410e-01 11.707 < 2e-16 ***
factor(id)84 1.710e+00 1.400e-01 12.214 < 2e-16 ***
factor(id)85 1.194e+00 1.413e-01 8.452 < 2e-16 ***
factor(id)86 1.491e+00 1.399e-01 10.661 < 2e-16 ***
factor(id)87 1.049e+00 1.426e-01 7.354 2.35e-13 ***
factor(id)88 1.215e+00 1.401e-01 8.669 < 2e-16 ***
factor(id)89 1.492e+00 1.406e-01 10.612 < 2e-16 ***
factor(id)90 1.429e+00 1.413e-01 10.115 < 2e-16 ***
factor(id)91 1.206e+00 1.396e-01 8.640 < 2e-16 ***
factor(id)92 1.558e+00 1.406e-01 11.082 < 2e-16 ***
factor(id)93 1.751e+00 1.422e-01 12.312 < 2e-16 ***
factor(id)94 1.728e+00 1.402e-01 12.327 < 2e-16 ***
factor(id)95 1.573e+00 1.398e-01 11.250 < 2e-16 ***
factor(id)96 2.075e+00 1.401e-01 14.812 < 2e-16 ***
factor(id)97 1.526e+00 1.400e-01 10.897 < 2e-16 ***
factor(id)98 1.874e+00 1.407e-01 13.318 < 2e-16 ***
factor(id)99 1.741e+00 1.396e-01 12.472 < 2e-16 ***
factor(id)100 2.157e+00 1.400e-01 15.408 < 2e-16 ***
factor(id)101 2.087e+00 1.402e-01 14.887 < 2e-16 ***
factor(id)102 1.832e+00 1.390e-01 13.178 < 2e-16 ***
factor(id)103 1.072e+00 1.386e-01 7.736 1.31e-14 ***
factor(id)104 1.393e+00 1.408e-01 9.898 < 2e-16 ***
factor(id)105 2.552e+00 1.401e-01 18.215 < 2e-16 ***
factor(id)106 1.115e+00 1.396e-01 7.989 1.78e-15 ***
factor(id)107 1.900e+00 1.402e-01 13.545 < 2e-16 ***
factor(id)108 1.339e+00 1.400e-01 9.565 < 2e-16 ***
factor(id)109 1.707e+00 1.410e-01 12.101 < 2e-16 ***
factor(id)110 1.452e+00 1.387e-01 10.469 < 2e-16 ***
factor(id)111 1.853e+00 1.417e-01 13.073 < 2e-16 ***
factor(id)112 1.700e+00 1.421e-01 11.964 < 2e-16 ***
factor(id)113 1.997e+00 1.394e-01 14.327 < 2e-16 ***
factor(id)114 1.143e+00 1.402e-01 8.152 4.79e-16 ***
factor(id)115 1.835e+00 1.418e-01 12.945 < 2e-16 ***
factor(id)116 1.515e+00 1.397e-01 10.847 < 2e-16 ***
factor(id)117 1.679e+00 1.443e-01 11.635 < 2e-16 ***
factor(id)118 1.374e+00 1.379e-01 9.969 < 2e-16 ***
factor(id)119 1.982e+00 1.402e-01 14.130 < 2e-16 ***
factor(id)120 2.333e+00 1.403e-01 16.626 < 2e-16 ***
factor(id)121 1.764e+00 1.398e-01 12.620 < 2e-16 ***
factor(id)122 1.698e+00 1.394e-01 12.180 < 2e-16 ***
factor(id)123 2.116e+00 1.409e-01 15.022 < 2e-16 ***
factor(id)124 3.344e-01 1.394e-01 2.398 0.016514 *
factor(id)125 1.083e+00 1.414e-01 7.658 2.37e-14 ***
factor(id)126 2.279e+00 1.400e-01 16.280 < 2e-16 ***
factor(id)127 1.372e+00 1.400e-01 9.804 < 2e-16 ***
factor(id)128 1.629e+00 1.398e-01 11.650 < 2e-16 ***
factor(id)129 1.669e+00 1.409e-01 11.845 < 2e-16 ***
factor(id)130 1.826e+00 1.423e-01 12.831 < 2e-16 ***
factor(id)131 2.243e+00 1.405e-01 15.960 < 2e-16 ***
factor(id)132 1.448e+00 1.399e-01 10.349 < 2e-16 ***
factor(id)133 1.154e+00 1.396e-01 8.261 < 2e-16 ***
factor(id)134 1.131e+00 1.392e-01 8.125 5.97e-16 ***
factor(id)135 2.035e+00 1.405e-01 14.485 < 2e-16 ***
factor(id)136 2.016e+00 1.405e-01 14.348 < 2e-16 ***
factor(id)137 1.839e+00 1.401e-01 13.131 < 2e-16 ***
factor(id)138 1.489e+00 1.399e-01 10.644 < 2e-16 ***
factor(id)139 1.736e+00 1.399e-01 12.413 < 2e-16 ***
factor(id)140 1.241e+00 1.390e-01 8.926 < 2e-16 ***
factor(id)141 1.067e+00 1.392e-01 7.668 2.21e-14 ***
factor(id)142 1.717e+00 1.404e-01 12.227 < 2e-16 ***
factor(id)143 2.174e+00 1.403e-01 15.494 < 2e-16 ***
factor(id)144 1.199e+00 1.455e-01 8.241 2.32e-16 ***
factor(id)145 1.574e+00 1.409e-01 11.171 < 2e-16 ***
factor(id)146 1.834e+00 1.411e-01 12.991 < 2e-16 ***
factor(id)147 1.319e+00 1.400e-01 9.422 < 2e-16 ***
factor(id)148 2.021e+00 1.401e-01 14.424 < 2e-16 ***
factor(id)149 1.622e+00 1.403e-01 11.567 < 2e-16 ***
factor(id)150 1.163e+00 1.407e-01 8.270 < 2e-16 ***
factor(id)151 2.226e+00 1.400e-01 15.900 < 2e-16 ***
factor(id)152 1.304e+00 1.416e-01 9.208 < 2e-16 ***
factor(id)153 2.283e+00 1.402e-01 16.290 < 2e-16 ***
factor(id)154 1.108e+00 1.403e-01 7.893 3.83e-15 ***
factor(id)155 9.691e-01 1.413e-01 6.860 8.00e-12 ***
factor(id)156 1.453e+00 1.400e-01 10.378 < 2e-16 ***
factor(id)157 1.716e+00 1.398e-01 12.279 < 2e-16 ***
factor(id)158 1.617e+00 1.405e-01 11.510 < 2e-16 ***
factor(id)159 2.082e+00 1.392e-01 14.963 < 2e-16 ***
factor(id)160 1.294e+00 1.400e-01 9.241 < 2e-16 ***
factor(id)161 1.464e+00 1.401e-01 10.445 < 2e-16 ***
factor(id)162 1.863e+00 1.407e-01 13.247 < 2e-16 ***
factor(id)163 1.778e+00 1.399e-01 12.708 < 2e-16 ***
factor(id)164 2.002e+00 1.396e-01 14.341 < 2e-16 ***
factor(id)165 1.891e+00 1.422e-01 13.297 < 2e-16 ***
factor(id)166 2.150e+00 1.395e-01 15.414 < 2e-16 ***
factor(id)167 1.067e+00 1.392e-01 7.662 2.31e-14 ***
factor(id)168 1.539e+00 1.387e-01 11.100 < 2e-16 ***
factor(id)169 1.196e+00 1.400e-01 8.548 < 2e-16 ***
factor(id)170 1.568e+00 1.395e-01 11.244 < 2e-16 ***
factor(id)171 1.674e+00 1.426e-01 11.740 < 2e-16 ***
factor(id)172 1.751e+00 1.411e-01 12.407 < 2e-16 ***
factor(id)173 2.264e+00 1.408e-01 16.077 < 2e-16 ***
factor(id)174 2.221e+00 1.402e-01 15.842 < 2e-16 ***
factor(id)175 1.775e+00 1.414e-01 12.547 < 2e-16 ***
factor(id)176 2.361e+00 1.400e-01 16.867 < 2e-16 ***
factor(id)177 1.784e+00 1.407e-01 12.680 < 2e-16 ***
factor(id)178 9.877e-01 1.407e-01 7.018 2.66e-12 ***
factor(id)179 7.941e-01 1.395e-01 5.691 1.36e-08 ***
factor(id)180 1.910e+00 1.400e-01 13.646 < 2e-16 ***
factor(id)181 2.093e+00 1.398e-01 14.972 < 2e-16 ***
factor(id)182 1.775e+00 1.393e-01 12.741 < 2e-16 ***
factor(id)183 2.011e+00 1.406e-01 14.302 < 2e-16 ***
factor(id)184 1.898e+00 1.398e-01 13.575 < 2e-16 ***
factor(id)185 1.884e+00 1.410e-01 13.361 < 2e-16 ***
factor(id)186 1.606e+00 1.392e-01 11.537 < 2e-16 ***
factor(id)187 1.841e+00 1.401e-01 13.143 < 2e-16 ***
factor(id)188 1.578e+00 1.405e-01 11.230 < 2e-16 ***
factor(id)189 2.079e+00 1.402e-01 14.825 < 2e-16 ***
factor(id)190 1.963e+00 1.386e-01 14.161 < 2e-16 ***
factor(id)191 1.444e+00 1.392e-01 10.373 < 2e-16 ***
factor(id)192 1.462e+00 1.400e-01 10.438 < 2e-16 ***
factor(id)193 1.786e+00 1.386e-01 12.892 < 2e-16 ***
factor(id)194 1.390e+00 1.409e-01 9.864 < 2e-16 ***
factor(id)195 8.809e-01 1.375e-01 6.406 1.68e-10 ***
factor(id)196 1.660e+00 1.403e-01 11.831 < 2e-16 ***
factor(id)197 1.788e+00 1.386e-01 12.904 < 2e-16 ***
factor(id)198 1.813e+00 1.393e-01 13.015 < 2e-16 ***
factor(id)199 1.740e+00 1.399e-01 12.436 < 2e-16 ***
factor(id)200 1.730e+00 1.393e-01 12.424 < 2e-16 ***
factor(id)201 2.524e+00 1.395e-01 18.096 < 2e-16 ***
factor(id)202 1.174e+00 1.393e-01 8.432 < 2e-16 ***
factor(id)203 1.215e+00 1.393e-01 8.726 < 2e-16 ***
factor(id)204 1.746e+00 1.411e-01 12.378 < 2e-16 ***
factor(id)205 1.806e+00 1.406e-01 12.839 < 2e-16 ***
factor(id)206 1.829e+00 1.419e-01 12.888 < 2e-16 ***
factor(id)207 1.874e+00 1.398e-01 13.401 < 2e-16 ***
factor(id)208 1.621e+00 1.405e-01 11.539 < 2e-16 ***
factor(id)209 1.965e+00 1.407e-01 13.968 < 2e-16 ***
factor(id)210 1.496e+00 1.395e-01 10.719 < 2e-16 ***
factor(id)211 1.063e+00 1.395e-01 7.623 3.12e-14 ***
factor(id)212 1.906e+00 1.406e-01 13.558 < 2e-16 ***
factor(id)213 1.442e+00 1.402e-01 10.284 < 2e-16 ***
factor(id)214 2.195e+00 1.404e-01 15.638 < 2e-16 ***
factor(id)215 1.597e+00 1.398e-01 11.425 < 2e-16 ***
factor(id)216 2.107e+00 1.400e-01 15.050 < 2e-16 ***
factor(id)217 2.296e+00 1.382e-01 16.612 < 2e-16 ***
factor(id)218 1.735e+00 1.399e-01 12.400 < 2e-16 ***
factor(id)219 2.044e+00 1.399e-01 14.608 < 2e-16 ***
factor(id)220 1.842e+00 1.399e-01 13.167 < 2e-16 ***
factor(id)221 2.098e+00 1.400e-01 14.987 < 2e-16 ***
factor(id)222 1.562e+00 1.399e-01 11.162 < 2e-16 ***
factor(id)223 1.889e+00 1.390e-01 13.597 < 2e-16 ***
factor(id)224 1.609e+00 1.411e-01 11.405 < 2e-16 ***
factor(id)225 1.953e+00 1.403e-01 13.917 < 2e-16 ***
factor(id)226 2.024e+00 1.412e-01 14.331 < 2e-16 ***
factor(id)227 2.148e+00 1.406e-01 15.282 < 2e-16 ***
factor(id)228 7.610e-01 1.389e-01 5.478 4.57e-08 ***
factor(id)229 1.648e+00 1.401e-01 11.765 < 2e-16 ***
factor(id)230 2.164e+00 1.424e-01 15.196 < 2e-16 ***
factor(id)231 1.953e+00 1.410e-01 13.854 < 2e-16 ***
factor(id)232 1.717e+00 1.404e-01 12.229 < 2e-16 ***
factor(id)233 1.791e+00 1.400e-01 12.799 < 2e-16 ***
factor(id)234 1.924e+00 1.408e-01 13.665 < 2e-16 ***
factor(id)235 1.877e+00 1.398e-01 13.423 < 2e-16 ***
factor(id)236 2.054e+00 1.402e-01 14.649 < 2e-16 ***
factor(id)237 1.377e+00 1.398e-01 9.851 < 2e-16 ***
factor(id)238 1.642e+00 1.405e-01 11.686 < 2e-16 ***
factor(id)239 2.352e+00 1.396e-01 16.854 < 2e-16 ***
factor(id)240 1.858e+00 1.403e-01 13.241 < 2e-16 ***
factor(id)241 1.303e+00 1.391e-01 9.368 < 2e-16 ***
factor(id)242 1.721e+00 1.422e-01 12.104 < 2e-16 ***
factor(id)243 1.643e+00 1.402e-01 11.713 < 2e-16 ***
factor(id)244 2.042e+00 1.400e-01 14.583 < 2e-16 ***
factor(id)245 1.352e+00 1.398e-01 9.667 < 2e-16 ***
factor(id)246 1.419e+00 1.413e-01 10.046 < 2e-16 ***
factor(id)247 1.495e+00 1.424e-01 10.497 < 2e-16 ***
factor(id)248 2.519e+00 1.403e-01 17.953 < 2e-16 ***
factor(id)249 2.531e+00 1.399e-01 18.087 < 2e-16 ***
factor(id)250 2.048e+00 1.400e-01 14.625 < 2e-16 ***
factor(id)251 1.288e+00 1.394e-01 9.241 < 2e-16 ***
factor(id)252 1.428e+00 1.407e-01 10.146 < 2e-16 ***
factor(id)253 1.873e+00 1.402e-01 13.362 < 2e-16 ***
factor(id)254 1.410e+00 1.402e-01 10.056 < 2e-16 ***
factor(id)255 1.509e+00 1.418e-01 10.643 < 2e-16 ***
factor(id)256 1.993e+00 1.403e-01 14.209 < 2e-16 ***
factor(id)257 1.911e+00 1.396e-01 13.689 < 2e-16 ***
factor(id)258 1.184e+00 1.415e-01 8.367 < 2e-16 ***
factor(id)259 1.773e+00 1.404e-01 12.632 < 2e-16 ***
factor(id)260 1.772e+00 1.427e-01 12.417 < 2e-16 ***
factor(id)261 1.071e+00 1.380e-01 7.758 1.10e-14 ***
factor(id)262 1.814e+00 1.404e-01 12.920 < 2e-16 ***
factor(id)263 1.300e+00 1.401e-01 9.278 < 2e-16 ***
factor(id)264 8.232e-01 1.385e-01 5.945 3.00e-09 ***
factor(id)265 1.521e+00 1.399e-01 10.873 < 2e-16 ***
factor(id)266 1.735e+00 1.395e-01 12.434 < 2e-16 ***
factor(id)267 1.191e+00 1.401e-01 8.501 < 2e-16 ***
factor(id)268 2.020e+00 1.408e-01 14.341 < 2e-16 ***
factor(id)269 1.939e+00 1.393e-01 13.917 < 2e-16 ***
factor(id)270 1.853e+00 1.390e-01 13.332 < 2e-16 ***
factor(id)271 1.393e+00 1.407e-01 9.899 < 2e-16 ***
factor(id)272 1.303e+00 1.402e-01 9.297 < 2e-16 ***
factor(id)273 2.135e+00 1.395e-01 15.303 < 2e-16 ***
factor(id)274 2.009e+00 1.397e-01 14.385 < 2e-16 ***
factor(id)275 1.382e+00 1.384e-01 9.988 < 2e-16 ***
factor(id)276 1.666e+00 1.416e-01 11.764 < 2e-16 ***
factor(id)277 1.320e+00 1.401e-01 9.420 < 2e-16 ***
factor(id)278 2.165e+00 1.400e-01 15.461 < 2e-16 ***
factor(id)279 1.372e+00 1.408e-01 9.739 < 2e-16 ***
factor(id)280 2.221e+00 1.400e-01 15.865 < 2e-16 ***
factor(id)281 1.767e+00 1.401e-01 12.611 < 2e-16 ***
factor(id)282 1.782e+00 1.414e-01 12.605 < 2e-16 ***
factor(id)283 1.311e+00 1.405e-01 9.333 < 2e-16 ***
factor(id)284 1.324e+00 1.402e-01 9.445 < 2e-16 ***
factor(id)285 1.051e+00 1.384e-01 7.598 3.75e-14 ***
factor(id)286 2.216e+00 1.398e-01 15.852 < 2e-16 ***
factor(id)287 1.226e+00 1.391e-01 8.816 < 2e-16 ***
factor(id)288 2.122e+00 1.400e-01 15.159 < 2e-16 ***
factor(id)289 1.599e+00 1.402e-01 11.407 < 2e-16 ***
factor(id)290 1.647e+00 1.403e-01 11.737 < 2e-16 ***
factor(id)291 1.373e+00 1.431e-01 9.594 < 2e-16 ***
factor(id)292 1.399e+00 1.400e-01 9.996 < 2e-16 ***
factor(id)293 1.120e+00 1.406e-01 7.965 2.17e-15 ***
factor(id)294 1.582e+00 1.409e-01 11.222 < 2e-16 ***
factor(id)295 1.179e+00 1.394e-01 8.456 < 2e-16 ***
factor(id)296 2.352e+00 1.403e-01 16.762 < 2e-16 ***
factor(id)297 2.279e+00 1.402e-01 16.257 < 2e-16 ***
factor(id)298 1.466e+00 1.433e-01 10.229 < 2e-16 ***
factor(id)299 1.836e+00 1.409e-01 13.033 < 2e-16 ***
factor(id)300 1.953e+00 1.407e-01 13.882 < 2e-16 ***
factor(id)301 2.216e+00 1.409e-01 15.728 < 2e-16 ***
factor(id)302 1.850e+00 1.399e-01 13.224 < 2e-16 ***
factor(id)303 1.739e+00 1.398e-01 12.446 < 2e-16 ***
factor(id)304 1.619e+00 1.414e-01 11.450 < 2e-16 ***
factor(id)305 1.650e+00 1.402e-01 11.768 < 2e-16 ***
factor(id)306 1.390e+00 1.415e-01 9.825 < 2e-16 ***
factor(id)307 1.322e+00 1.417e-01 9.329 < 2e-16 ***
factor(id)308 1.667e+00 1.404e-01 11.877 < 2e-16 ***
factor(id)309 2.002e+00 1.413e-01 14.169 < 2e-16 ***
factor(id)310 1.502e+00 1.416e-01 10.609 < 2e-16 ***
factor(id)311 1.434e+00 1.401e-01 10.232 < 2e-16 ***
factor(id)312 9.779e-01 1.396e-01 7.005 2.90e-12 ***
factor(id)313 1.342e+00 1.400e-01 9.584 < 2e-16 ***
factor(id)314 1.577e+00 1.397e-01 11.291 < 2e-16 ***
factor(id)315 1.530e+00 1.418e-01 10.784 < 2e-16 ***
factor(id)316 1.352e+00 1.395e-01 9.688 < 2e-16 ***
factor(id)317 1.258e+00 1.409e-01 8.925 < 2e-16 ***
factor(id)318 1.507e+00 1.413e-01 10.664 < 2e-16 ***
factor(id)319 1.437e+00 1.418e-01 10.133 < 2e-16 ***
factor(id)320 1.315e+00 1.406e-01 9.352 < 2e-16 ***
factor(id)321 1.680e+00 1.398e-01 12.014 < 2e-16 ***
factor(id)322 1.927e+00 1.414e-01 13.630 < 2e-16 ***
factor(id)323 1.447e+00 1.397e-01 10.358 < 2e-16 ***
factor(id)324 1.653e+00 1.420e-01 11.644 < 2e-16 ***
factor(id)325 1.805e+00 1.397e-01 12.921 < 2e-16 ***
factor(id)326 1.572e+00 1.401e-01 11.218 < 2e-16 ***
factor(id)327 1.948e+00 1.410e-01 13.818 < 2e-16 ***
factor(id)328 1.317e+00 1.409e-01 9.350 < 2e-16 ***
factor(id)329 1.777e+00 1.403e-01 12.663 < 2e-16 ***
factor(id)330 1.847e+00 1.397e-01 13.224 < 2e-16 ***
factor(id)331 1.914e+00 1.396e-01 13.709 < 2e-16 ***
factor(id)332 1.518e+00 1.400e-01 10.842 < 2e-16 ***
factor(id)333 1.725e+00 1.400e-01 12.320 < 2e-16 ***
factor(id)334 1.673e+00 1.399e-01 11.956 < 2e-16 ***
factor(id)335 1.233e+00 1.424e-01 8.661 < 2e-16 ***
factor(id)336 1.373e+00 1.402e-01 9.793 < 2e-16 ***
factor(id)337 1.249e+00 1.406e-01 8.888 < 2e-16 ***
factor(id)338 1.307e+00 1.391e-01 9.399 < 2e-16 ***
factor(id)339 1.633e+00 1.406e-01 11.615 < 2e-16 ***
factor(id)340 1.669e+00 1.397e-01 11.942 < 2e-16 ***
factor(id)341 1.989e+00 1.400e-01 14.209 < 2e-16 ***
factor(id)342 7.782e-01 1.417e-01 5.492 4.24e-08 ***
factor(id)343 7.649e-01 1.399e-01 5.466 4.89e-08 ***
factor(id)344 1.091e+00 1.401e-01 7.782 9.09e-15 ***
factor(id)345 1.593e+00 1.429e-01 11.149 < 2e-16 ***
factor(id)346 1.717e+00 1.401e-01 12.250 < 2e-16 ***
factor(id)347 1.800e+00 1.401e-01 12.846 < 2e-16 ***
factor(id)348 1.450e+00 1.395e-01 10.400 < 2e-16 ***
factor(id)349 1.851e+00 1.402e-01 13.208 < 2e-16 ***
factor(id)350 1.161e+00 1.392e-01 8.345 < 2e-16 ***
factor(id)351 2.047e+00 1.399e-01 14.632 < 2e-16 ***
factor(id)352 1.816e+00 1.406e-01 12.923 < 2e-16 ***
factor(id)353 2.172e+00 1.409e-01 15.414 < 2e-16 ***
factor(id)354 1.244e+00 1.398e-01 8.896 < 2e-16 ***
factor(id)355 2.019e+00 1.401e-01 14.415 < 2e-16 ***
factor(id)356 1.467e+00 1.400e-01 10.476 < 2e-16 ***
factor(id)357 1.600e+00 1.400e-01 11.430 < 2e-16 ***
factor(id)358 1.302e+00 1.415e-01 9.202 < 2e-16 ***
factor(id)359 1.698e+00 1.408e-01 12.057 < 2e-16 ***
factor(id)360 1.807e+00 1.408e-01 12.832 < 2e-16 ***
factor(id)361 1.837e+00 1.451e-01 12.660 < 2e-16 ***
factor(id)362 1.482e+00 1.394e-01 10.630 < 2e-16 ***
factor(id)363 2.686e+00 1.407e-01 19.096 < 2e-16 ***
factor(id)364 2.075e+00 1.400e-01 14.817 < 2e-16 ***
factor(id)365 1.734e+00 1.400e-01 12.387 < 2e-16 ***
factor(id)366 1.715e+00 1.400e-01 12.248 < 2e-16 ***
factor(id)367 1.018e+00 1.395e-01 7.297 3.55e-13 ***
factor(id)368 1.391e+00 1.394e-01 9.979 < 2e-16 ***
factor(id)369 1.410e+00 1.400e-01 10.071 < 2e-16 ***
factor(id)370 1.409e+00 1.397e-01 10.081 < 2e-16 ***
factor(id)371 1.666e+00 1.410e-01 11.815 < 2e-16 ***
factor(id)372 1.219e+00 1.407e-01 8.665 < 2e-16 ***
factor(id)373 1.963e+00 1.396e-01 14.061 < 2e-16 ***
factor(id)374 1.415e+00 1.413e-01 10.013 < 2e-16 ***
factor(id)375 1.925e+00 1.403e-01 13.718 < 2e-16 ***
factor(id)376 1.605e+00 1.414e-01 11.358 < 2e-16 ***
factor(id)377 1.592e+00 1.422e-01 11.194 < 2e-16 ***
factor(id)378 1.783e+00 1.400e-01 12.734 < 2e-16 ***
factor(id)379 1.309e+00 1.440e-01 9.088 < 2e-16 ***
factor(id)380 1.897e+00 1.410e-01 13.452 < 2e-16 ***
factor(id)381 1.581e+00 1.387e-01 11.406 < 2e-16 ***
factor(id)382 3.175e+00 1.393e-01 22.796 < 2e-16 ***
factor(id)383 1.219e+00 1.389e-01 8.775 < 2e-16 ***
factor(id)384 1.769e+00 1.411e-01 12.532 < 2e-16 ***
factor(id)385 2.302e+00 1.405e-01 16.388 < 2e-16 ***
factor(id)386 1.732e+00 1.403e-01 12.346 < 2e-16 ***
factor(id)387 2.297e+00 1.400e-01 16.409 < 2e-16 ***
factor(id)388 1.802e+00 1.400e-01 12.867 < 2e-16 ***
factor(id)389 2.019e+00 1.410e-01 14.323 < 2e-16 ***
factor(id)390 1.593e+00 1.400e-01 11.381 < 2e-16 ***
factor(id)391 1.384e+00 1.401e-01 9.878 < 2e-16 ***
factor(id)392 2.439e+00 1.409e-01 17.310 < 2e-16 ***
factor(id)393 1.571e+00 1.402e-01 11.200 < 2e-16 ***
factor(id)394 1.505e+00 1.401e-01 10.745 < 2e-16 ***
factor(id)395 1.448e+00 1.402e-01 10.330 < 2e-16 ***
factor(id)396 1.377e+00 1.407e-01 9.783 < 2e-16 ***
factor(id)397 1.845e+00 1.402e-01 13.162 < 2e-16 ***
factor(id)398 1.497e+00 1.398e-01 10.710 < 2e-16 ***
factor(id)399 2.313e+00 1.408e-01 16.434 < 2e-16 ***
factor(id)400 1.224e+00 1.409e-01 8.690 < 2e-16 ***
factor(id)401 1.804e+00 1.416e-01 12.739 < 2e-16 ***
factor(id)402 2.198e+00 1.405e-01 15.648 < 2e-16 ***
factor(id)403 1.715e+00 1.400e-01 12.244 < 2e-16 ***
factor(id)404 1.699e+00 1.408e-01 12.069 < 2e-16 ***
factor(id)405 1.531e+00 1.397e-01 10.964 < 2e-16 ***
factor(id)406 2.051e+00 1.400e-01 14.650 < 2e-16 ***
factor(id)407 1.423e+00 1.411e-01 10.085 < 2e-16 ***
factor(id)408 1.456e+00 1.431e-01 10.177 < 2e-16 ***
factor(id)409 1.566e+00 1.400e-01 11.184 < 2e-16 ***
factor(id)410 1.326e+00 1.392e-01 9.530 < 2e-16 ***
factor(id)411 1.088e+00 1.393e-01 7.815 7.08e-15 ***
factor(id)412 9.472e-01 1.398e-01 6.774 1.45e-11 ***
factor(id)413 2.315e+00 1.398e-01 16.562 < 2e-16 ***
factor(id)414 8.820e-01 1.448e-01 6.092 1.23e-09 ***
factor(id)415 1.235e+00 1.398e-01 8.837 < 2e-16 ***
factor(id)416 1.254e+00 1.398e-01 8.968 < 2e-16 ***
factor(id)417 1.849e+00 1.403e-01 13.180 < 2e-16 ***
factor(id)418 1.394e+00 1.419e-01 9.825 < 2e-16 ***
factor(id)419 9.013e-01 1.407e-01 6.407 1.67e-10 ***
factor(id)420 1.391e+00 1.405e-01 9.900 < 2e-16 ***
factor(id)421 7.832e-01 1.400e-01 5.595 2.36e-08 ***
factor(id)422 1.735e+00 1.396e-01 12.430 < 2e-16 ***
factor(id)423 1.388e+00 1.412e-01 9.830 < 2e-16 ***
factor(id)424 1.697e+00 1.397e-01 12.146 < 2e-16 ***
factor(id)425 1.695e+00 1.430e-01 11.848 < 2e-16 ***
factor(id)426 1.529e+00 1.396e-01 10.948 < 2e-16 ***
factor(id)427 1.715e+00 1.411e-01 12.150 < 2e-16 ***
factor(id)428 2.054e+00 1.379e-01 14.897 < 2e-16 ***
factor(id)429 1.551e+00 1.401e-01 11.067 < 2e-16 ***
factor(id)430 1.369e+00 1.400e-01 9.777 < 2e-16 ***
factor(id)431 1.434e+00 1.403e-01 10.218 < 2e-16 ***
factor(id)432 1.238e+00 1.398e-01 8.853 < 2e-16 ***
factor(id)433 1.594e+00 1.402e-01 11.370 < 2e-16 ***
factor(id)434 2.363e+00 1.401e-01 16.866 < 2e-16 ***
factor(id)435 1.620e+00 1.402e-01 11.554 < 2e-16 ***
factor(id)436 9.913e-01 1.398e-01 7.091 1.58e-12 ***
factor(id)437 1.253e+00 1.426e-01 8.793 < 2e-16 ***
factor(id)438 1.066e+00 1.400e-01 7.615 3.29e-14 ***
factor(id)439 1.874e+00 1.439e-01 13.026 < 2e-16 ***
factor(id)440 2.082e+00 1.407e-01 14.789 < 2e-16 ***
factor(id)441 2.173e+00 1.400e-01 15.525 < 2e-16 ***
factor(id)442 1.622e+00 1.402e-01 11.572 < 2e-16 ***
factor(id)443 1.527e+00 1.444e-01 10.577 < 2e-16 ***
factor(id)444 2.185e+00 1.400e-01 15.602 < 2e-16 ***
factor(id)445 1.124e+00 1.429e-01 7.868 4.66e-15 ***
factor(id)446 1.357e+00 1.396e-01 9.721 < 2e-16 ***
factor(id)447 1.340e+00 1.404e-01 9.542 < 2e-16 ***
factor(id)448 1.545e+00 1.399e-01 11.045 < 2e-16 ***
factor(id)449 2.378e+00 1.396e-01 17.032 < 2e-16 ***
factor(id)450 1.193e+00 1.409e-01 8.463 < 2e-16 ***
factor(id)451 1.338e+00 1.439e-01 9.297 < 2e-16 ***
factor(id)452 1.425e+00 1.395e-01 10.214 < 2e-16 ***
factor(id)453 1.694e+00 1.402e-01 12.081 < 2e-16 ***
factor(id)454 1.402e+00 1.396e-01 10.046 < 2e-16 ***
factor(id)455 1.835e+00 1.407e-01 13.037 < 2e-16 ***
factor(id)456 1.503e+00 1.401e-01 10.730 < 2e-16 ***
factor(id)457 2.358e+00 1.407e-01 16.759 < 2e-16 ***
factor(id)458 2.015e+00 1.402e-01 14.369 < 2e-16 ***
factor(id)459 1.641e+00 1.395e-01 11.768 < 2e-16 ***
factor(id)460 1.551e+00 1.394e-01 11.124 < 2e-16 ***
factor(id)461 2.027e+00 1.402e-01 14.457 < 2e-16 ***
factor(id)462 1.757e+00 1.401e-01 12.547 < 2e-16 ***
factor(id)463 1.959e+00 1.406e-01 13.932 < 2e-16 ***
factor(id)464 1.024e+00 1.400e-01 7.311 3.20e-13 ***
factor(id)465 1.125e+00 1.406e-01 8.004 1.58e-15 ***
factor(id)466 1.627e+00 1.384e-01 11.761 < 2e-16 ***
factor(id)467 2.347e+00 1.396e-01 16.810 < 2e-16 ***
factor(id)468 1.161e+00 1.446e-01 8.030 1.29e-15 ***
factor(id)469 2.123e+00 1.397e-01 15.199 < 2e-16 ***
factor(id)470 1.340e+00 1.405e-01 9.538 < 2e-16 ***
factor(id)471 2.196e+00 1.382e-01 15.891 < 2e-16 ***
factor(id)472 1.569e+00 1.409e-01 11.134 < 2e-16 ***
factor(id)473 1.916e+00 1.407e-01 13.622 < 2e-16 ***
factor(id)474 2.626e+00 1.454e-01 18.065 < 2e-16 ***
factor(id)475 2.197e+00 1.402e-01 15.667 < 2e-16 ***
factor(id)476 1.859e+00 1.404e-01 13.244 < 2e-16 ***
factor(id)477 1.604e+00 1.421e-01 11.284 < 2e-16 ***
factor(id)478 1.707e+00 1.397e-01 12.217 < 2e-16 ***
factor(id)479 1.091e+00 1.464e-01 7.454 1.12e-13 ***
factor(id)480 2.014e+00 1.409e-01 14.297 < 2e-16 ***
factor(id)481 1.278e+00 1.408e-01 9.072 < 2e-16 ***
factor(id)482 1.245e+00 1.395e-01 8.929 < 2e-16 ***
factor(id)483 1.960e+00 1.429e-01 13.719 < 2e-16 ***
factor(id)484 1.972e+00 1.412e-01 13.967 < 2e-16 ***
factor(id)485 2.230e+00 1.402e-01 15.899 < 2e-16 ***
factor(id)486 1.769e+00 1.401e-01 12.630 < 2e-16 ***
factor(id)487 2.108e+00 1.406e-01 14.992 < 2e-16 ***
factor(id)488 1.473e+00 1.406e-01 10.476 < 2e-16 ***
factor(id)489 9.278e-01 1.414e-01 6.560 6.12e-11 ***
factor(id)490 1.740e+00 1.398e-01 12.443 < 2e-16 ***
factor(id)491 1.731e+00 1.411e-01 12.266 < 2e-16 ***
factor(id)492 1.089e+00 1.389e-01 7.835 6.05e-15 ***
factor(id)493 1.520e+00 1.403e-01 10.834 < 2e-16 ***
factor(id)494 1.707e+00 1.400e-01 12.195 < 2e-16 ***
factor(id)495 1.256e+00 1.401e-01 8.965 < 2e-16 ***
factor(id)496 1.730e+00 1.402e-01 12.343 < 2e-16 ***
factor(id)497 2.238e+00 1.402e-01 15.968 < 2e-16 ***
factor(id)498 1.575e+00 1.403e-01 11.225 < 2e-16 ***
factor(id)499 1.530e+00 1.409e-01 10.857 < 2e-16 ***
factor(id)500 1.168e+00 1.396e-01 8.370 < 2e-16 ***
factor(id)501 2.247e+00 1.423e-01 15.789 < 2e-16 ***
factor(id)502 1.389e+00 1.396e-01 9.949 < 2e-16 ***
factor(id)503 1.676e+00 1.391e-01 12.048 < 2e-16 ***
factor(id)504 1.600e+00 1.399e-01 11.436 < 2e-16 ***
factor(id)505 1.149e+00 1.420e-01 8.090 7.92e-16 ***
factor(id)506 9.673e-01 1.395e-01 6.932 4.84e-12 ***
factor(id)507 1.813e+00 1.407e-01 12.886 < 2e-16 ***
factor(id)508 4.152e-01 1.399e-01 2.968 0.003015 **
factor(id)509 1.254e+00 1.400e-01 8.956 < 2e-16 ***
factor(id)510 8.598e-01 1.392e-01 6.175 7.32e-10 ***
factor(id)511 1.279e+00 1.393e-01 9.178 < 2e-16 ***
factor(id)512 1.472e+00 1.383e-01 10.646 < 2e-16 ***
factor(id)513 1.579e+00 1.409e-01 11.205 < 2e-16 ***
factor(id)514 2.003e+00 1.404e-01 14.269 < 2e-16 ***
factor(id)515 2.164e+00 1.415e-01 15.294 < 2e-16 ***
factor(id)516 1.545e+00 1.374e-01 11.246 < 2e-16 ***
factor(id)517 1.546e+00 1.409e-01 10.975 < 2e-16 ***
factor(id)518 2.192e+00 1.397e-01 15.690 < 2e-16 ***
factor(id)519 1.562e+00 1.494e-01 10.453 < 2e-16 ***
factor(id)520 1.644e+00 1.428e-01 11.517 < 2e-16 ***
factor(id)521 1.094e+00 1.400e-01 7.819 6.85e-15 ***
factor(id)522 1.648e+00 1.406e-01 11.723 < 2e-16 ***
factor(id)523 2.240e+00 1.394e-01 16.072 < 2e-16 ***
factor(id)524 1.506e+00 1.408e-01 10.700 < 2e-16 ***
factor(id)525 1.773e+00 1.390e-01 12.755 < 2e-16 ***
factor(id)526 1.487e+00 1.382e-01 10.757 < 2e-16 ***
factor(id)527 1.856e+00 1.407e-01 13.190 < 2e-16 ***
factor(id)528 1.433e+00 1.391e-01 10.301 < 2e-16 ***
factor(id)529 1.311e+00 1.391e-01 9.427 < 2e-16 ***
factor(id)530 1.174e+00 1.423e-01 8.251 < 2e-16 ***
factor(id)531 1.493e+00 1.389e-01 10.752 < 2e-16 ***
factor(id)532 1.839e+00 1.393e-01 13.204 < 2e-16 ***
factor(id)533 1.969e+00 1.405e-01 14.013 < 2e-16 ***
factor(id)534 7.982e-01 1.402e-01 5.694 1.33e-08 ***
factor(id)535 1.137e+00 1.414e-01 8.042 1.17e-15 ***
factor(id)536 1.715e+00 1.408e-01 12.181 < 2e-16 ***
factor(id)537 1.803e+00 1.417e-01 12.723 < 2e-16 ***
factor(id)538 1.284e+00 1.408e-01 9.116 < 2e-16 ***
factor(id)539 2.039e+00 1.405e-01 14.518 < 2e-16 ***
factor(id)540 1.617e+00 1.391e-01 11.629 < 2e-16 ***
factor(id)541 1.655e+00 1.390e-01 11.910 < 2e-16 ***
factor(id)542 2.179e+00 1.399e-01 15.582 < 2e-16 ***
factor(id)543 1.317e+00 1.418e-01 9.289 < 2e-16 ***
factor(id)544 2.172e+00 1.399e-01 15.531 < 2e-16 ***
factor(id)545 1.383e+00 1.405e-01 9.849 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3873 on 3814 degrees of freedom
Multiple R-squared: 0.9563, Adjusted R-squared: 0.9501
F-statistic: 152.9 on 546 and 3814 DF, p-value: < 2.2e-16
Построим оценку сквозного МНК. Проверим значимость коэффициентов, используя ковариационную матрицу ошибок Хубера – Уайта.
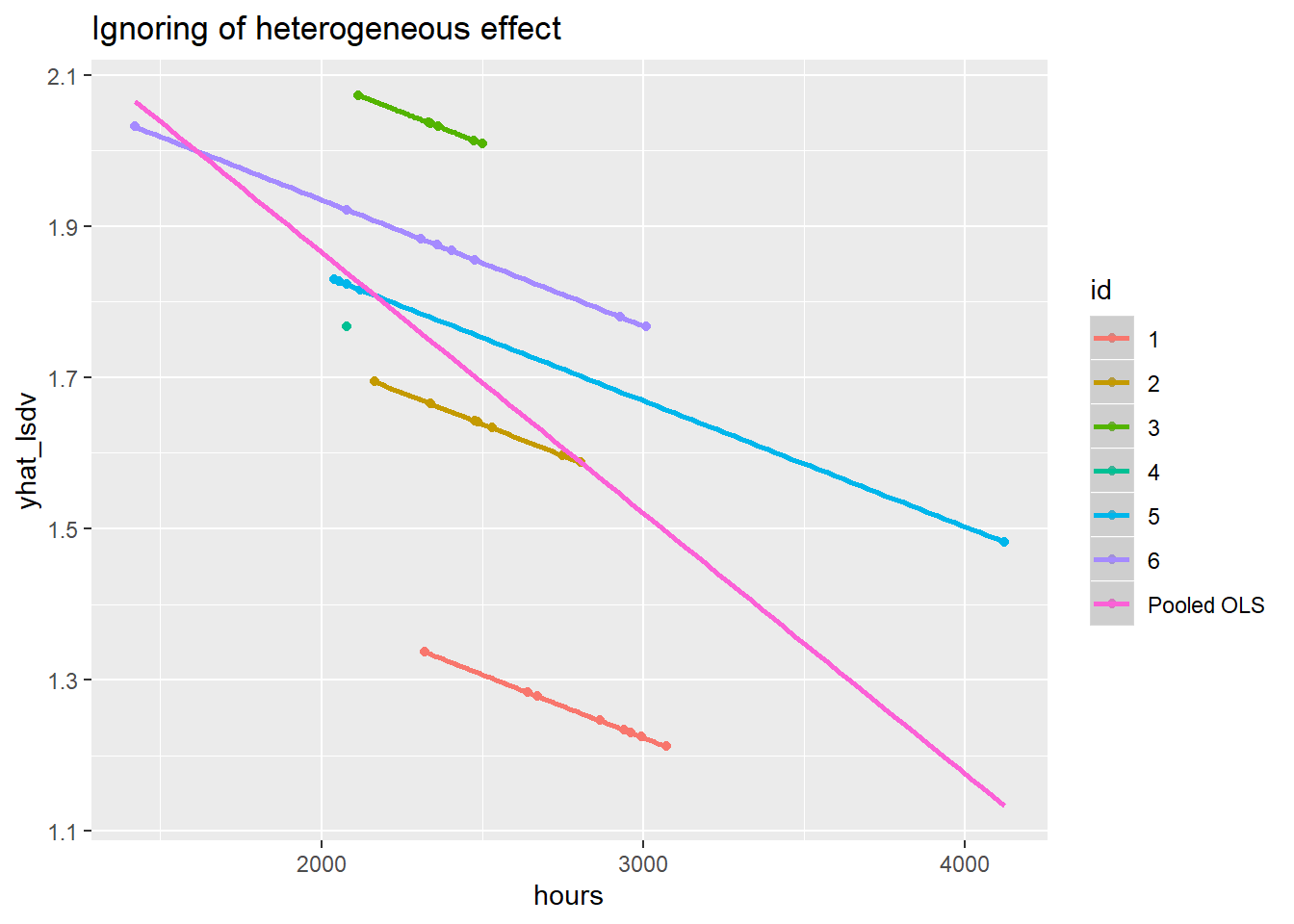
Покажем, что эта модель игнорирует гетерогенный эффект.
fpo = plm(lwage ~ hours, model = "pooling",data = Panel)
coeftest(fpo, vcov = vcovHC(fpo, cluster = "group"))
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.6286e+00 6.2980e-02 25.860 <2e-16 ***
hours 9.3560e-06 2.7040e-05 0.346 0.7294
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(fpo)
Pooling Model
Call:
plm(formula = lwage ~ hours, data = Panel, model = "pooling")
Balanced Panel: n = 545, T = 8, N = 4360
Residuals:
Min. 1st Qu. Median 3rd Qu. Max.
-5.226250 -0.297525 0.021354 0.342911 2.414420
Coefficients:
Estimate Std. Error t-value Pr(>|t|)
(Intercept) 1.6286e+00 3.2240e-02 50.5170 <2e-16 ***
hours 9.3560e-06 1.4245e-05 0.6568 0.5113
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Total Sum of Squares: 1236.5
Residual Sum of Squares: 1236.4
R-Squared: 9.8978e-05
Adj. R-Squared: -0.00013046
F-statistic: 0.431389 on 1 and 4358 DF, p-value: 0.51134
panel = import("../data/09_small.csv")
panel = mutate(panel, black = factor(black), id = factor(id))
lsdv_small = lm(lwage ~ hours + factor(id) - 1, data = panel)
yhat_lsdv = lsdv_small$fitted.values
g = ggplot(panel, aes(hours, yhat_lsdv, col = id))
g + geom_point() +
geom_smooth(aes(group = id, col = id), method = "lm") +
geom_smooth(aes(col = "Pooled OLS"),method = "lm", se = FALSE) +
labs(title = "Ignoring of heterogeneous effect")
Python
import numpy as np
import pandas as pd
Подгрузим данные и для обозначения панельных данных присвоим соответствующие индексы.
Зададим соответствующие зависимые и независимые переменные, а также регрессионную формулу.
Переменная “Entity effects” (Фиксированные эффекты) обязательна для включения для корректного распознавания панельных данных.
Если её не включить, результат будет отличаться от R и STATA.
df = pd.read_csv('../data/09_large.csv')
df = df.set_index(['id', 'year'])
formula = 'lwage ~ 1 + hours + EntityEffects'
dependent = df.lwage
regressors = df[['hours']]
print(df.head())
nr black exper hisp ... union lwage expersq occupation
id year ...
1 1980 13 0 1 0 ... 0 1.197540 1 9
1981 13 0 2 0 ... 1 1.853060 4 9
1982 13 0 3 0 ... 0 1.344462 9 9
1983 13 0 4 0 ... 0 1.433213 16 9
1984 13 0 5 0 ... 0 1.568125 25 5
[5 rows x 11 columns]
Оценим FE-модель, используя within-оценку.
from linearmodels import PanelOLS
C:\Users\The_sun\ANACON~1\lib\site-packages\linearmodels\panel\data.py:10: FutureWarning: The Panel class is removed from pandas. Accessing it from the top-level namespace will also be removed in the next version
from pandas import (Categorical, DataFrame, Index, MultiIndex, Panel, Series,
model_fe = PanelOLS.from_formula(formula, df)
model_fe_fitted = model_fe.fit(cov_type='clustered', cluster_entity=True)
print(model_fe_fitted)
PanelOLS Estimation Summary
================================================================================
Dep. Variable: lwage R-squared: 4.166e-07
Estimator: PanelOLS R-squared (Between): -2.301e-05
No. Observations: 4360 R-squared (Within): 4.166e-07
Date: Sat, Jan 25 2020 R-squared (Overall): -1.217e-05
Time: 19:53:27 Log-likelihood -1759.0
Cov. Estimator: Clustered
F-statistic: 0.0016
Entities: 545 P-value 0.9682
Avg Obs: 8.0000 Distribution: F(1,3814)
Min Obs: 8.0000
Max Obs: 8.0000 F-statistic (robust): 0.0005
P-value 0.9822
Time periods: 8 Distribution: F(1,3814)
Avg Obs: 545.00
Min Obs: 545.00
Max Obs: 545.00
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 1.6504 0.0549 30.058 0.0000 1.5427 1.7580
hours -5.585e-07 2.506e-05 -0.0223 0.9822 -4.968e-05 4.857e-05
==============================================================================
F-test for Poolability: 8.1423
P-value: 0.0000
Distribution: F(544,3814)
Included effects: Entity
Оценим RE-модель, используя FGLS-оценку.
from linearmodels.panel import RandomEffects
model_re = RandomEffects.from_formula(formula, df)
model_re_fitted = model_re.fit(cov_type='clustered', cluster_entity=True)
dir(model_re_fitted)
print(model_re_fitted)
RandomEffects Estimation Summary
================================================================================
Dep. Variable: lwage R-squared: 2.749e-06
Estimator: RandomEffects R-squared (Between): 5.737e-05
No. Observations: 4360 R-squared (Within): -5.03e-06
Date: Sat, Jan 25 2020 R-squared (Overall): 2.85e-05
Time: 19:53:28 Log-likelihood -2049.3
Cov. Estimator: Clustered
F-statistic: 0.0120
Entities: 545 P-value 0.9128
Avg Obs: 8.0000 Distribution: F(1,4358)
Min Obs: 8.0000
Max Obs: 8.0000 F-statistic (robust): 0.0038
P-value 0.9510
Time periods: 8 Distribution: F(1,4358)
Avg Obs: 545.00
Min Obs: 545.00
Max Obs: 545.00
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 1.6459 0.0549 29.972 0.0000 1.5383 1.7536
hours 1.461e-06 2.375e-05 0.0615 0.9510 -4.511e-05 4.803e-05
==============================================================================
Тест Хаусмана в соответствующем пакете на данный момент не реализован.
Построим оценку Pooled OLS
from linearmodels.panel import PooledOLS
model_pool = PooledOLS.from_formula(formula, df)
model_pool_fitted = model_pool.fit(cov_type='clustered', cluster_entity=True)
print(model_pool_fitted)
PooledOLS Estimation Summary
================================================================================
Dep. Variable: lwage R-squared: 9.898e-05
Estimator: PooledOLS R-squared (Between): 0.0003
No. Observations: 4360 R-squared (Within): -0.0001
Date: Sat, Jan 25 2020 R-squared (Overall): 9.898e-05
Time: 19:53:28 Log-likelihood -3439.2
Cov. Estimator: Clustered
F-statistic: 0.4314
Entities: 545 P-value 0.5113
Avg Obs: 8.0000 Distribution: F(1,4358)
Min Obs: 8.0000
Max Obs: 8.0000 F-statistic (robust): 0.1197
P-value 0.7294
Time periods: 8 Distribution: F(1,4358)
Avg Obs: 545.00
Min Obs: 545.00
Max Obs: 545.00
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
Intercept 1.6286 0.0630 25.854 0.0000 1.5051 1.7521
hours 9.356e-06 2.705e-05 0.3459 0.7294 -4.367e-05 6.238e-05
==============================================================================
Построим LSDV-оценку.
model_lsdv = PanelOLS.from_formula(formula, df)
model_lsdv_fitted = model_lsdv.fit(cov_type='clustered', cluster_entity=True, use_lsdv=True)
print(model_lsdv_fitted)
Построим FD-оценку. Здесь необходимо убрать константный признак, так как данная модель начинает выдавать ошибку. Логически, конечно, он автоматически должен исчезнуть по построению модели, но в данной реализации это требуется задать на уровне пользователя.
from linearmodels.panel import FirstDifferenceOLS
formula_fd = 'lwage ~ hours + EntityEffects'
model_fd = FirstDifferenceOLS.from_formula(formula_fd, df)
model_fd_fitted = model_fd.fit(cov_type='clustered', cluster_entity=True)
print(model_fd_fitted)
FirstDifferenceOLS Estimation Summary
================================================================================
Dep. Variable: lwage R-squared: 0.0483
Estimator: FirstDifferenceOLS R-squared (Between): -0.5823
No. Observations: 3815 R-squared (Within): -0.0547
Date: Sat, Jan 25 2020 R-squared (Overall): -0.5593
Time: 19:53:28 Log-likelihood -2262.7
Cov. Estimator: Clustered
F-statistic: 193.77
Entities: 545 P-value 0.0000
Avg Obs: 8.0000 Distribution: F(1,3814)
Min Obs: 8.0000
Max Obs: 8.0000 F-statistic (robust): 66.959
P-value 0.0000
Time periods: 8 Distribution: F(1,3814)
Avg Obs: 545.00
Min Obs: 545.00
Max Obs: 545.00
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
hours -0.0002 2.481e-05 -8.1828 0.0000 -0.0003 -0.0002
==============================================================================
Stata
Теперь то же самое в Stata
Для начала подгрузим данные и посмотрим на них. Сперва визуализируем малый датасет.
use data/09_small
summarize
file data/09_small.dta not found
r(601);
end of do-file
r(601);
xtset id year
xtline hours, overlay
clear
no variables defined
r(111);
end of do-file
r(111);
use data/09_large
xtset id year
summarize
file data/09_large.dta not found
r(601);
end of do-file
r(601);
Визуализируем данные. Если необходимо разнести линии на разные графики, следует убрать прараметр “overlay”.
Сгенерируем новую переменную и оценим модель с фиксированными эффектами. Последний аргумент произведёт оценку стандартных ошибок переменных в форме Хубера - Уайта
xtreg lwage hours, fe vce(robust)
variable lwage not found
r(111);
end of do-file
r(111);
Сделаем то же самое для модели со случайными эффектами.
xtreg lwage hours, re vce(robust)
variable lwage not found
r(111);
end of do-file
r(111);
Тест Хаусмана.
xtreg lwage hours, re
estimates store b_re
xtreg lwage hours, fe
estimates store b_fe
hausman b_fe b_re, sigmamore
variable lwage not found
r(111);
end of do-file
r(111);
Оценим FD-модель.
reg D.(lwage hours), vce(robust) nocon
no variables defined
r(111);
end of do-file
r(111);
Аналогично оцениваем модель pooled OLS.
reg lwage hours, vce(robust)
no variables defined
r(111);
end of do-file
r(111);
Оценим LSDV-модель.
areg lwage hours, absorb(id)
no variables defined
(error in option absorb())
r(111);
end of do-file
r(111);



