13 Байесовский подход

конспект: Мария Салунина, Полина Лапшова

дата: 23 января 2017

13.1 Хинты к брутальной части (16 января 2017)

13.1.1 Первая задача

Дано:

\(\hat{y}=3+7x\)
\(R^2=0.6\)
\(sVar(y)=1000\)

Задание 1: найти \(sCov(y, x)\).

Мы знаем, что \(sVar(y)=\frac{\sum\limits_{i=1}^n(y_i-\overline{y})^2}{n-1}\).

Замечание: чем отличается \(Var(y)\) от \(sVar(y)\)? \(Var(y)\) - матрица из констант размера \(n \times n\). \(sVar(y)\) - вектор размера \(1 \times 1\), случайная величина.

Что такое \(R^2\)?

Первая интерпретация: доля объяснённой дисперсии.

\(R^2=\frac{sVar(\hat{y})}{sVar(y)}=0.6\), следовательно, \(sVar(\hat{y})=600\).

\(\hat{y}=3+7x\), т. е. \(\hat{y}\) в семь раз больше \(x\), значит:

\(sVar(x)=\frac{600}{49}\)
Вторая интерпретация: \(R^2=sCorr^2(y, \hat{y})\)

\(sCorr(y, \hat{y})=\sqrt{0.6}\)

\(sCorr(y, x)=+\sqrt{0.6}\)

Замечание: знак \("+"\), так как в регрессии перед \(x\) стоит плюс.

\(sCorr(y, x)=\frac{sCov(y, x)}{\sqrt{sVar(y)sVar(x)}}=+\sqrt{0.6}\)

\(sVar(y)=1000\)

\(sVar(x)=\frac{600}{49}\)

Следовательно, \(sCov(y, x)=85.7143\)

Итог: индивидуальные регрессии позволяют найти любую выборочную корреляцию, любую выборочную ковариацию, любую выборочную дисперсию.

Задание 2: найти регрессию \(y_i=\beta_1 +\beta_2 x_i +\beta_3 z_i + u_i\)

Как найти вектор \(\hat{\beta}\)?

\(\begin{pmatrix} \hat{\beta_1}\\ \hat{\beta_2}\\ \hat{\beta_3}\\ \end{pmatrix} = (X'X)^{-1}X'y\)

Фриша-Вау: проведём регрессию в два шага.

Отрегрессируем \(x\), \(z\), \(y\) на \(1\) (чтобы избавиться от единичного столбца)

Для \(x\):

\(x_i=c+u_i\)

тогда: \(\hat{c}=\overline{x}\),

\(\widetilde{x_i}=x_i-\overline{x}\) - остаток от регрессии \(x\).

\(\dots\)

Получим остатки от регрессий \(\widetilde{x}, \widetilde{z}, \widetilde{y}\).
Чтобы оценить \(\hat{\beta_2}\) и \(\hat{\beta_3}\), необходимо построить следующую регрессию.

\(\widetilde{y}\) на \(\widetilde{x}\), \(\widetilde{z}\)

\(\hat{\widetilde{y_i}}=\hat{\beta_2} \widetilde{x_i} + \hat{\beta_3} \widetilde{z_i}\)

Следовательно:

\(\begin{pmatrix} \hat{\beta_2}\\ \hat{\beta_3}\\ \end{pmatrix} = (\widetilde{X}'\widetilde{X})^{-1}\widetilde{X}'\widetilde{y}\)

\(\widetilde{y} = \left( \begin{matrix} y_1 - \overline{y}\\ \vdots\\ y_n - \overline{y}\\ \end{matrix} \right)\)

\(\widetilde{X} = \left( \begin{matrix} x_1 - \overline{x} & z_1 - \overline{z}\\ \vdots& \vdots\\ x_n - \overline{x} & z_n - \overline{z}\\ \end{matrix} \right)\)

\(\widetilde{X}^{'}\widetilde{X} = \left( \begin{matrix} \sum\limits_{i=1}^n(x_i-\overline{x})^2 & \sum\limits_{i=1}^n(x_i-\overline{x})(z_i-\overline{z})\\ \sum\limits_{i=1}^n(x_i-\overline{x})(z_i-\overline{z}) & \sum\limits_{i=1}^n(z_i-\overline{z})^2\\ \end{matrix} \right)\)

\(\widetilde{X}^{'}\widetilde{y} = \left( \begin{matrix} \sum\limits_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})\\ \sum\limits_{i=1}^n(z_i-\overline{z})(y_i-\overline{y})\\ \end{matrix} \right)\)

\(\left( \begin{matrix} \hat{\beta_2}\\ \hat{\beta_3}\\ \end{matrix} \right) = \left(\frac{\widetilde{X}^{'}\widetilde{X}}{n-1}\right)^{-1}\frac{\widetilde{X}^{'}\widetilde{y}}{n-1}\)

Средние были даны, любая регрессия проходит через среднюю линию, можно восстановить \(\hat{\beta_1}\).

13.1.2 Третья задача

Дано две модели:

\(\hat{y_i}=\hat{\beta_1}+\underset{(3.2)}{\hat{\beta_2}}x_i\)

\(\hat{y_i}=\hat{\gamma_1}+\hat{\gamma_2} x_i+\underset{(7.8)}{10}z_i\)

\(R^2=0.8\) (для второй модели)

Задание: проверить гипотезу \(H_0: \beta_2=0\).

Проверим сначала \(\gamma_3\):

\(t = \frac{10}{7.8}\)

Если знаем \(R^2\), то можем проверить значимость регрессии в целом.

\(t^2=F=\left(\frac{10}{7.8}\right)^2\)

Одинаковы ли регрессии.

\(F = \frac{(R_{UR}^2-R_R^2)/1}{R_{UR}^2/(n-k_{UR})}\)

Пояснение: единичка в знаменателе числителя — одно ограничение на вторую регрессию (\(\gamma_3=0\)).

Следовательно, получаем \(R_R^2\), можем проверить гипотезу о значимости.

Почему \(t^2=F\)?

\(y_i=\beta_1+\beta_2 x_i+u_i\)

\(t = \frac{\hat{\beta_2}}{se(\hat{\beta_2})} = \frac{sCov(x,y)}{sVar(x)}\frac{1}{\sqrt{\frac{RSS}{n-2}\frac{1}{\sum(x_i-\overline{x})^2}}}\)

\(RSS^2 = (1-R^2)*TSS = (1-sCorr^2(x,y))sVar(y)(n-1)\)

\(t^2=\frac{sCov^2(x,y)}{sVar(x)}\frac{(n-2)(n-1)}{(1-sCorr^2(x,y))sVar(y)(n-1)}=\frac{sCorr^2(x,y)/1}{(1-sCorr^2(x,y))/(n-2)}\)

\(H_0: \beta_2=0\) — одно ограничение. Проверяем одну и ту же гипотезу только с разных сторон.

\(F=\frac{R^2}{(1-R^2)/(n-2)}\) — вуаля! то же самое! Ч.Т.Д.

13.2 Отличие классического подхода от байесовского

13.2.1 Классический подход

\(\beta\) vs \(\hat{\beta}\)

\(\beta\) — неизвестный параметр \(const\) (не знаю и никогда не узнаю). \(P(\beta>0)\) — бессмысленный вопрос (данная вероятность равна либо \(0\), либо \(1\)).
Модель: как данные \(y_i\) зависят от \(\beta\).
Применяется метод (метод наименьших квадратов, метод моментов, метод максимального правдоподобия и т.д.); на основании модели получаем \(\hat{\beta}=f(y_1, y_2, \dots, y_n)\).
ЦПТ, ЗБЧ, \(\Delta\)-метод при \(n \to \infty\)

\(\hat{\beta} \sim \mathbb{N}(., .)\).

Итог: пункт 3 — точечная оценка \(\hat{\beta}\); пункт 4 — доверительный интервал \(\beta \in [\hat{\beta} - \dots; \hat{\beta} + \dots]\).

13.2.2 Байесовский подход

Есть только \(\beta\) — всё наше знание о неизвестном параметре сформулировано в виде закона распределения.

Априорное мнение о \(\beta\) до получения наблюдения. Существует \(P(\beta>0)\).
Модель: как данные \(y_i\) зависят от \(\beta\).
Используется формула условной вероятности. По формуле \(f(\beta\mid y_1, y_2, \dots, y_n)\) получается апостериорное распределение \(\beta\).

\(P(\beta>0\mid y_1, y_2, \dots, y_n)\) — можно найти.
Можно получить точечную и интервальную оценку.

13.2.3 Упражнение №1 (про шапку с монетками)

Условие: в шапке есть серебряные и золотые монетки; \(\beta\) — доля золотых монеток.

\(0 \leqslant \beta \leqslant 1\)

Предположим, \(\beta\) распределена равномерно: \(\beta \sim \mathbb{U}[0, 1]\)
\(y_i\) — наблюдения.

\[ y_i = \begin{cases} 0, & \text{если монетка серебряная;} \\ 1, & \text{если монетка золотая.} \end{cases} \]

Достаём, смотрим, какая монетка, отмечаем наблюдение, кидаем монетку обратно в шапку, перемешиваем.

$y_i \mid \beta$ — независимы



|$y_i \mid \beta$|0|1|
|-----------|---------|---------|
|*вероятность*|$1-\beta$| $\beta$ |




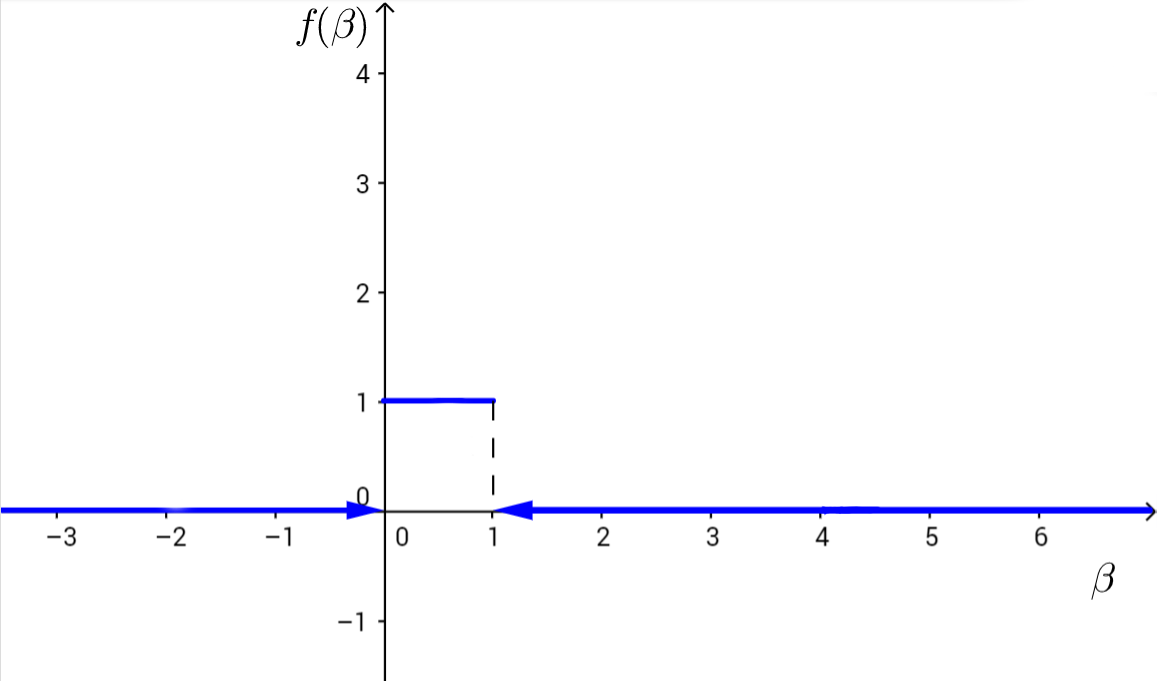
![*Функция плотности "до"*](images/16_1.png)



$y_1=1$

$y_2=1$

$f(\beta\mid y_1=1, y_2=1)=\frac{f(\beta, y_1=1, y_2=1)}{P(y_1=1,y_2=1)} \propto f(\beta, y_1=1, y_2=1) = P(y_1=1, y_2=1 \mid \beta)f(\beta)$

\[ P(y_1=1, y_2=1 \mid\mid \beta)f(\beta) = \begin{cases} \beta^2, & \beta \in [0;1], \\ 0, & \text{иначе.} \\ \end{cases} \]

\(\int\limits_0^1 \beta^2\,d\beta = \left. \frac{\beta^3}{3}\right|_0^1 = \frac{1}{3}\)

Следовательно, необходимо домножить на 3.

\[
f(\beta\mid y_1=1, y_2=1) =
\begin{cases}
3\beta^2, & \beta \in [0;1], \\
0, & \text{иначе.}
\end{cases}
\]


 
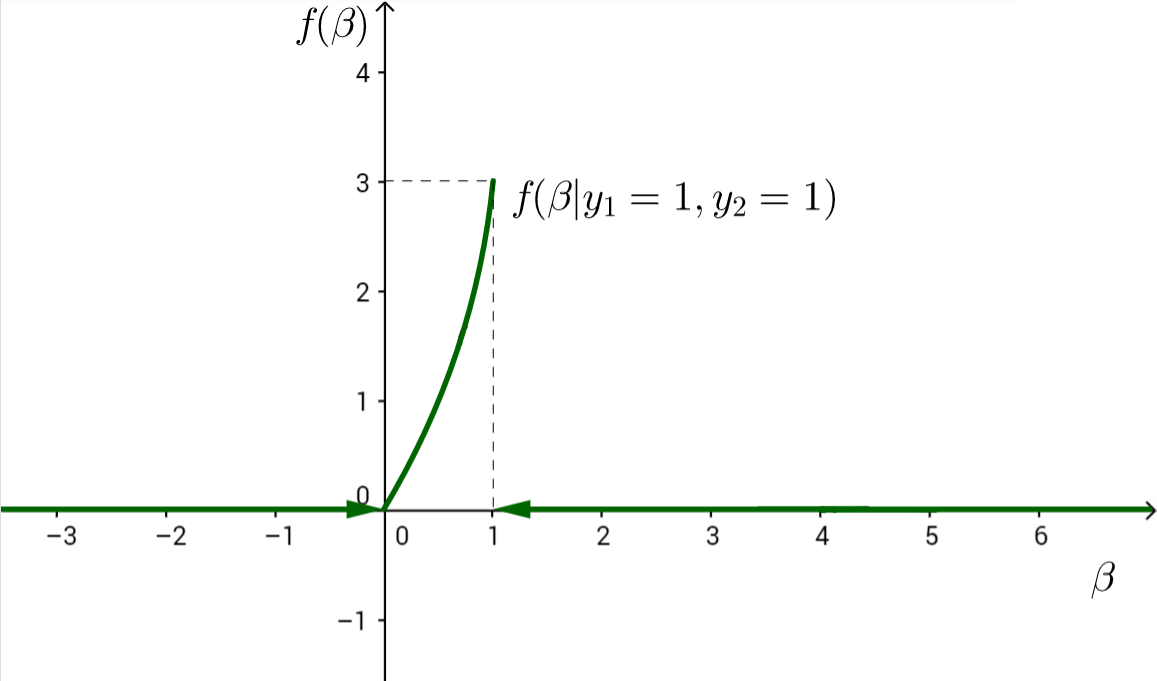
![*Функция плотности "после"*](images/16_2.png)



До наблюдений: $P(\beta>\frac{1}{2})=\frac{1}{2}$.

После наблюдений: $P(\beta>\frac{1}{2}\mid y_1=1, y_2=1)=\int\limits_\frac{1}{2}^1 3\beta^2\,d\beta = \frac{7}{8}$.

Точечная оценка: апостериорное мат. ожидание или медиана.

$\mathbb{E}(\beta\mid y_1=1, y_2=1) = \int\limits_0^1 \beta \cdot f(\beta\mid y_1=1, y_2=1)\,d\beta$

13.2.4 Упражнение №2 (про Машу и мышек)

Задача: где-то на числовой прямой, в точке \(m\), Маша прячет от мышек сыр. При этом известно, что её любимое число — 13.

\(m \sim \mathbb{N}(13, 100)\)
Прибежали две мышки и пропищали, где, по их мнению, наиболее сильно пахнет сыром: \(y_1=9\), \(y_2=18\).
- \(y_i\mid m\) — независимы;
- \(y_i=m+u_i\);
- \(y_i\mid m \sim \mathbb{N}(m, 25)\).
\(f(m)\propto e^{-(m-13)^2/(2*100)}\) — априорная функция плотности.

\(f(m\mid y_1=9,y_2=18) \propto f(m,y_1=9,y_2=18)=f(y_1=9,y_2=18\mid m)f(m) \propto e^{-(9-m)^2/(2*25)}e^{-(18-m)^2/(2*25)}e^{-(m-13)^2/(2*100)} \propto e^{-\frac{1}{2} * \frac{1}{100} * (9m^2-2m(13+9*4+18*4))} \propto e^{-\frac{1}{2} * \frac{1}{100/9} * (m-\frac{121}{9})^2}\) — функция плотности.

\(m \sim \mathbb{N}(\frac{121}{9}, \frac{100}{9})\)

Магия: \(\frac{121}{9}=\frac{4}{9}*9+\frac{4}{9}*18+\frac{4}{9}*13\)

13.2.4.1 Домашнее задание

Установить STAN bayesian.