3 Геометрия МНК

конспект: Света Колесниченко

дата: 19 сентября 2016

3.1 Обозначения

Варианты представления регрессии:

Скалярный вариант: $\hat y_{i} = \hat \beta_1 + \hat \beta_2\, x_{i} + \hat \beta_3\, z_{i}$
Векторный вариант: $\hat y = \hat \beta_1\, e + \hat \beta_2\, x + \hat \beta_3\, z$

\[ \begin{matrix} & e = \vec 1 = \\ \end{matrix} \begin{pmatrix} 1 \\ \vdots \\ 1 \end{pmatrix} \begin{matrix} \textit{ - единичный вектор размерности $n \times 1$}, \end{matrix} \]

\[ \begin{matrix} & x = \\ \end{matrix} \begin{pmatrix} x_{1} \\ \vdots \\ x_{n} \end{pmatrix} \begin{matrix} & y = \\ \end{matrix} \begin{pmatrix} y_{1} \\ \vdots \\ y_{n} \end{pmatrix} \begin{matrix} & z = \\ \end{matrix} \begin{pmatrix} z_{1} \\ \vdots \\ z_{n} \end{pmatrix} \textit{ - векторы переменных} \]
Количество наблюдений = $n$, количество коэффициентов $\beta$ = количество регрессоров = $k$.

Матричный вариант: $\hat y = X\, \hat \beta$

\[ \begin{matrix} & \hat \beta = \\ \end{matrix} \begin{pmatrix} \hat \beta_{1} \\ \vdots \\ \hat \beta_{k} \end{pmatrix} \begin{matrix} \textit{ - вектор размера } k\times 1, \end{matrix} \]

\[ \begin{matrix} & X = \\ \end{matrix} \begin{pmatrix} 1 & x_{1} & z_{1} \\ \vdots & \vdots & \vdots \\ 1 & x_n & z_{n} \end{pmatrix} \begin{matrix} \textit{ - матрица размера } n \times k \end{matrix} \]
Конвенция об обозначениях:

$y, \beta, \hat \beta, x, z$ - векторы
$y_{i}, \beta_{j}, \hat \beta_{7}, x_{45}, z_{37}$ - числа (скаляры)
$\Omega, X, H$ - матрицы

3.2 Ныряем в $n$-мерное пространство

\[ \min_{i\in I} \sum_{i=1}^n (y_{i} - \hat y_{i})^{2} = \min_{i\in I} \sum_{i=1}^n |y_{i} - \hat y_{i}|^{2} \textit{ - минимизируем квадрат длины вектора} \]

\[ \begin{pmatrix} \bar y \\ \vdots \\ \bar y \end{pmatrix} \begin{matrix} & = \bar y \cdot \\ \end{matrix} \begin{pmatrix} 1 \\ \vdots \\ 1 \end{pmatrix} \begin{matrix} & = \bar y \cdot \vec 1 \end{matrix} \]

$\bar y = \hat y$ - т.к. $\bar y \cdot \vec 1 = \hat y \cdot \vec 1$

среднее значение = среднее значение прогнозов ($\hat y_{i}$)

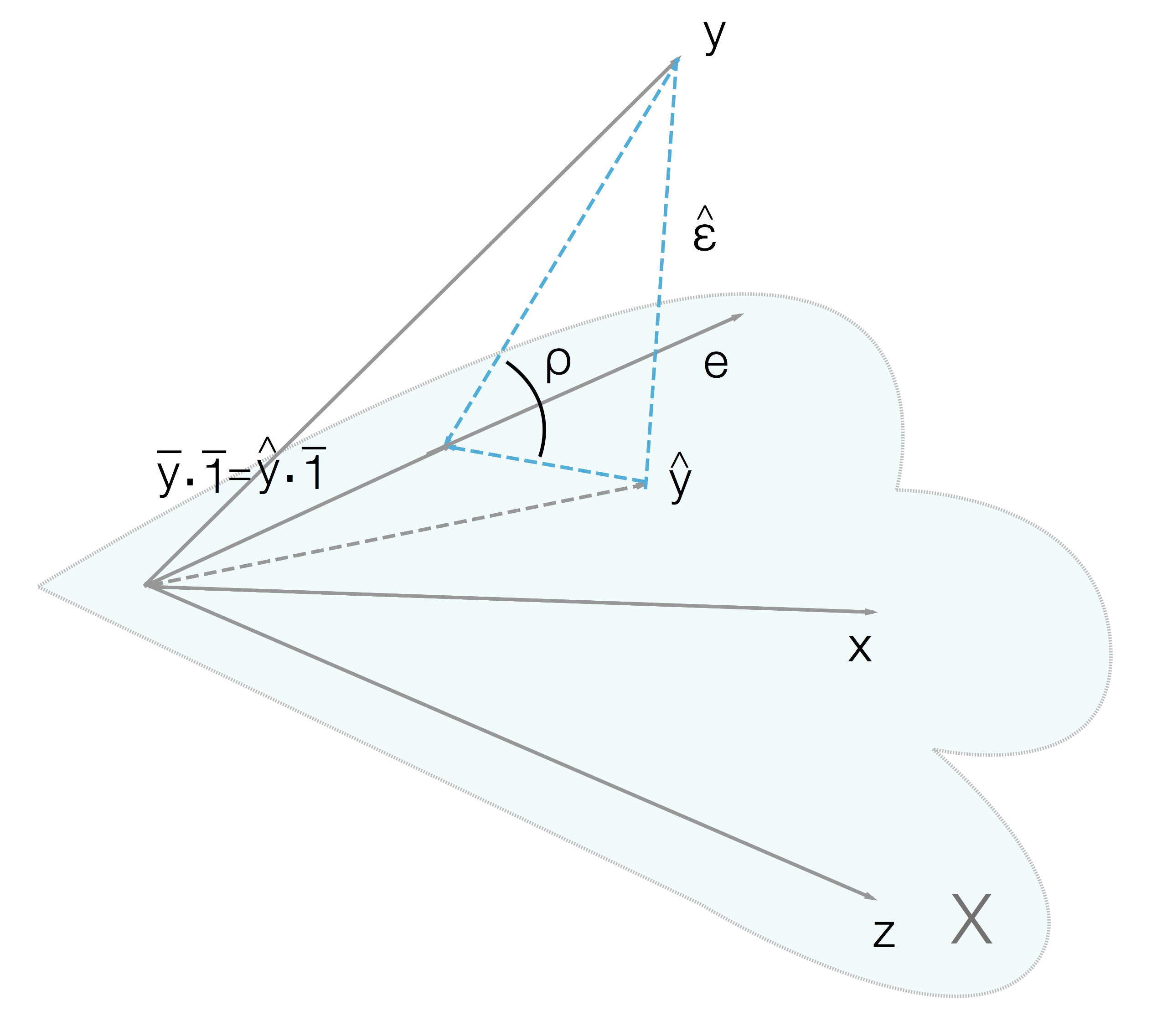
Картиночка Лапы

“Лапа” = $Lin (e, x, z) \leftarrow$ выбираем через e, x, z положение $\hat y$

$\hat y$ - проекция y на “лапу”

y - линейная комбинация e, x, z $\rightarrow$ лежит в линейной оболочке этих векторов

$\hat \varepsilon = y - \hat y$ - вектор “остатков”/ошибок прогнозов/resideals

$\hat \varepsilon \,\bot\, e, \hat \varepsilon \,\bot\, x, \hat \varepsilon \,\bot\, y$

$\hat \varepsilon \cdot \vec 1 = 0$, $\hat \varepsilon \cdot x = 0$, $\hat \varepsilon \cdot z = 0$ $\leftarrow$ скалярное произведение векторов (ссыль подробнее) перпендикулярных векторов равно 0.

$\hat \varepsilon \, \bot \, \textit{Лапа} \rightarrow \hat \varepsilon \, \bot \, \textit{любому вектору, лежащему в Лапе}$

Великая Теорема о 3 перпендикулярах и аж в 2 формулировках и с чертёжиком.

\[ \sum_{i=1}^n \hat \varepsilon_{i}=0 , \sum_{i=1}^n \hat \varepsilon_{i} x_{i}=0 \] \[ \begin{matrix} & X' = \\ \end{matrix} \begin{pmatrix} 1 & \dots & 1\\ x & \dots & x_{n} \\ z & \dots & z_{n} \end{pmatrix} \begin{matrix} \textit{ - единичный вектор размерности $n \times 1$} \end{matrix} \begin{matrix} & \hat \varepsilon = \\ \end{matrix} \begin{pmatrix} \hat \varepsilon_{1} \\ \vdots \\ \hat \varepsilon_{n} \end{pmatrix} \begin{matrix} \textit{ - единичный вектор размерности $n \times 1$} \end{matrix} \]

Условие ортогональности: $X' \cdot \hat \varepsilon = 0$ - размерность этого нуля - $k \times 1$

$\hat y = X \cdot \hat \beta \rightarrow \hat \beta = \frac{\hat y}{X} = \frac{\hat \varepsilon - Y}{X}$

3.2.1 Упражнение 1

Выведите $\hat \beta$ из $X'\cdot(y-X\cdot\hat \beta) = 0$

$\hat \varepsilon = y - \hat y = y - X\cdot\hat \beta$

$X$ - задает “лапу”.

$\hat \beta$ - отвечает за то, с каким весом в $\hat y$ входят базисные векторы «лапы».

$\hat \beta = (\sum_{i=1}^n x^2_{i})^{-1}\, \sum_{i=1}^n x_{i} y_{i}=0$ - для $\hat y_{i} = \hat \beta \, x_{i}$

$X'\cdot y = X'\cdot X\cdot \hat \beta$ $(X' \cdot X)^{-1}\cdot X' \cdot y = (X' \cdot X)^{-1}\cdot X'\cdot X \cdot \hat \beta$ $\hat \beta = (X' \cdot X)^{-1}\cdot X'\cdot y$

3.3 Больше проекций

3.3.1 Упражнение 2

Спроецируйте вектор $\,\begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix}\,$ на прямую, порождённую вектором $\,\begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix}\,.$

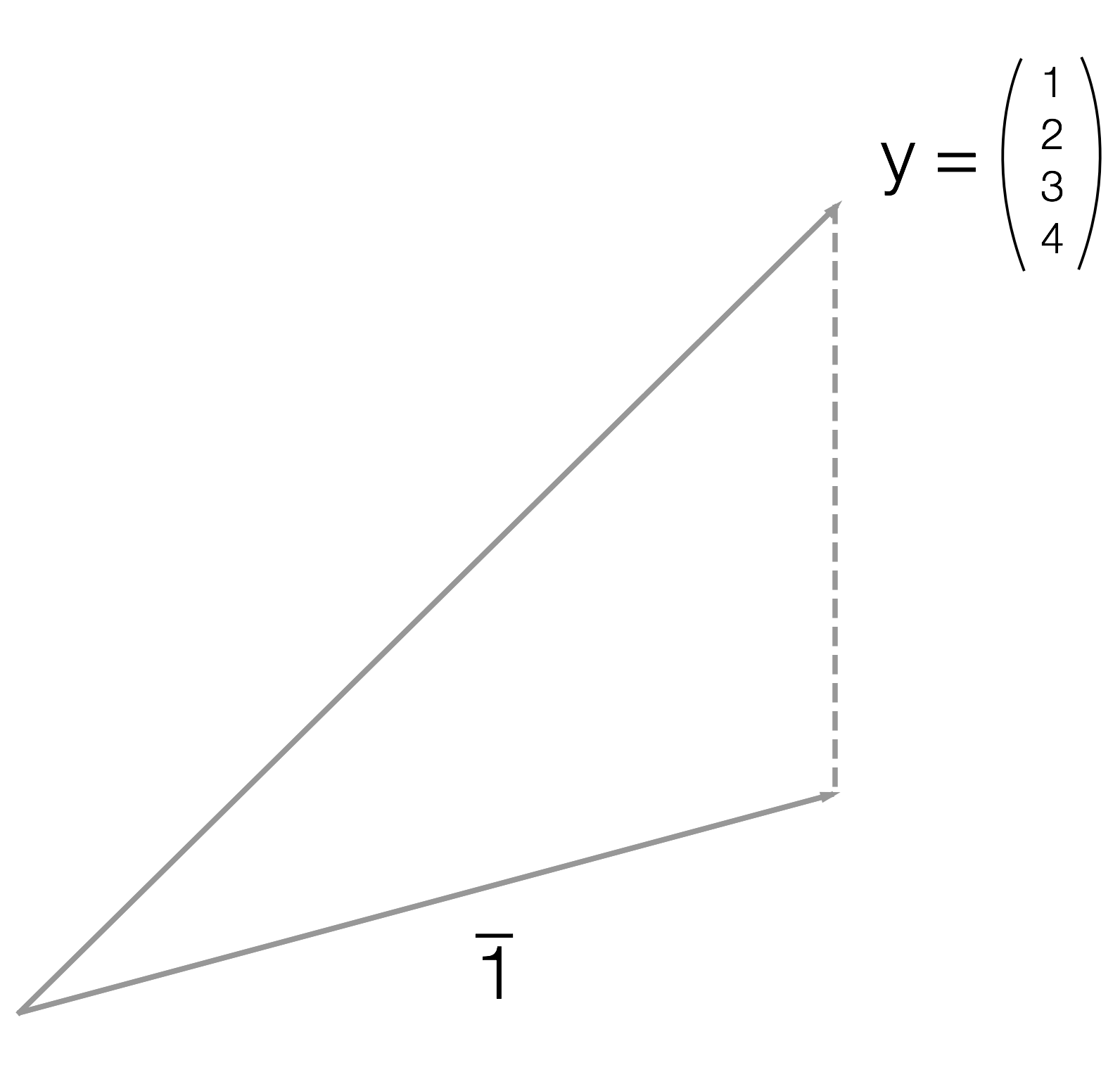
Визуализация задачи

\[ \begin{matrix} & \hat \beta = \\ \end{matrix} \begin{pmatrix} 1 & 1 & 1 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} \begin{matrix} = 4^{-1} \cdot 10 \cdot \frac{1}{4} \cdot 10 = 2.5 \\ \end{matrix} \]

\[ \begin{matrix} & \hat y = X \cdot \hat \beta = \\ \end{matrix} \begin{pmatrix} 2.5 \\ 2.5 \\ 2.5 \\ 2.5 \end{pmatrix} \begin{matrix} = \\ \end{matrix} \begin{pmatrix} \bar y \\ \bar y \\ \bar y \\ \bar y \end{pmatrix} \]

\[ \bar y = \frac{1+2+3+4}{4} = 2.5 \]

Проекция вектора на прямую из единиц даёт вектор из средних.

By the way, крутые читщиты по матрицам и основам линейной алгебры.

3.3.2 Упражнение 3

Сформулируйте все теоремы Пифагора

$\{\hat \varepsilon, \hat y - \bar y \cdot \vec 1, y - \bar y \cdot \vec 1\}\,$

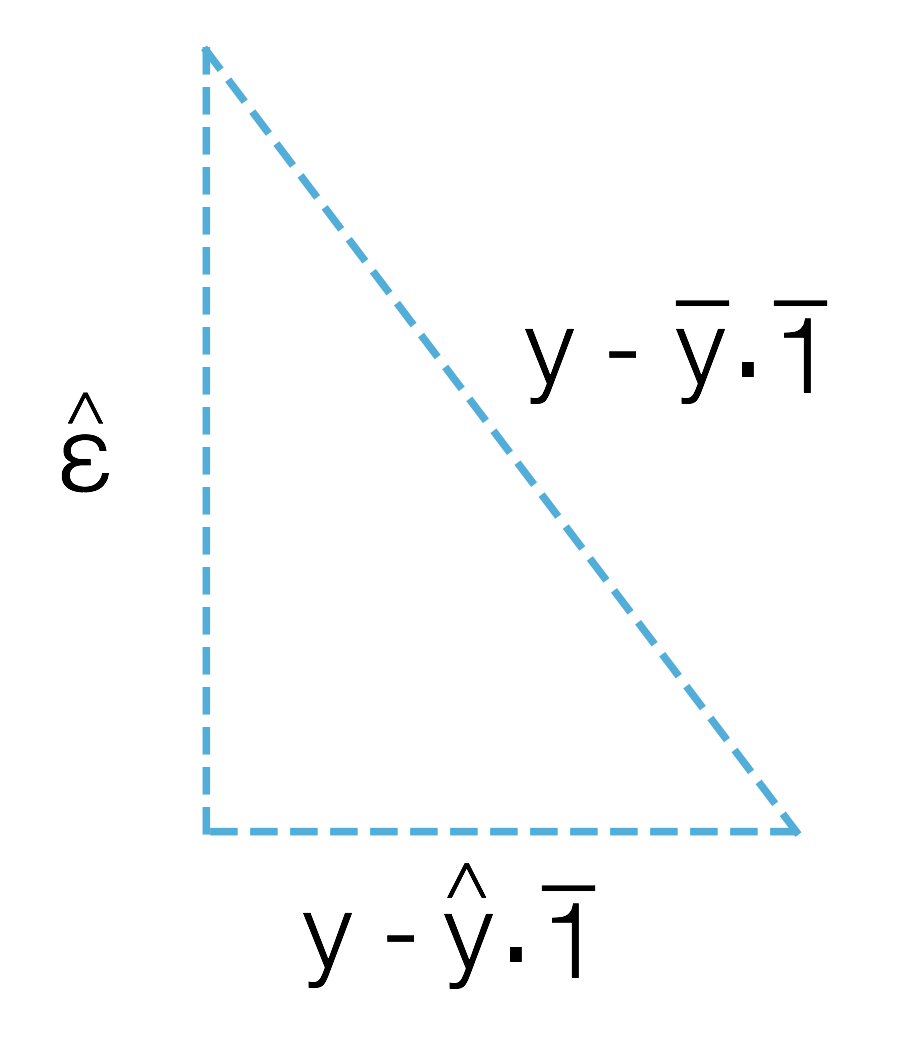
Чертёжик одного из треугольников

По Теореме Пифагора:

\[ |y - \bar y \cdot \vec 1|^{2} = |\hat \varepsilon|^2 + |\hat y - \bar y \cdot \vec 1|^2 \] \[ \sum_{i=1}^n (y_{i}- \bar y)^2 = \sum_{i=1}^n \hat \varepsilon^2_{i} + \sum_{i=1}^n (\hat y_{i}- \bar y)^2 \] \[ \begin{matrix} & y_{i}- \bar y = \\ \end{matrix} \begin{pmatrix} y_{1} - \bar y\\ \vdots \\ y_{n} - \bar y \end{pmatrix} \]

Полное задание см. в Задачнике по координатам: 4.23, 4.24, 4.25

Коэффициент детерминации ($R^2$) - примитивный показатель качества прогнозов.

\[ R^2 = \frac{ESS}{TSS} = \frac{\sum_{i=1}^n \hat \varepsilon^2_{i}}{\sum_{i=1}^n (y_{i}- \bar y)^2} = \frac{\sum_{i=1}^n (y_{i}- \hat y)^2}{\sum_{i=1}^n (y_{i}- \bar y)^2} = \frac{\text{residial sum of squares (cумма квадратов остатков)}}{\text{total sum of squares (полная сумма квадратов)}} \]

\[ ESS = \sum_{i=1}^n (\hat y_{i}- \bar y)^2 = \, \text{explained sum of squares ("объясненная" сумма квадратов)} \]

В МНК работает (и точно только в нём!) соотношение: $RSS + ESS = TSS$.

В МНК решается задача минимизации RSS.

Если прогнозы $\hat y_i$ идеально совпадают с $y_i$, то $R^2 = 1 \Rightarrow ESS = TSS$.

$R^2 \in [0;1]\, , R^2 = \cos^2 \rho$

$\hat y$ ближе к $y$ с ростом «лапы» $\Rightarrow$ $\angle \rho \downarrow \, \rightarrow R^2\,$ т.к. $\cos^2 \rho \uparrow$

3.3.2.1 ДЗ:

1.1, 1.2, 1.7, 1.12, 1.13, 4.13 (1-6), 4.23, 4.24, 4.25 из Задачника

3.3.2.1.1 Полезные ссылки:

Репозиторий курса метрики и теории вероятностей

Конспект семинаров по метрике-2016