Глава 8 Условное математическое ожидание от сигма–алгебры
Конспект: Ксения Кинякина
дата: 7 октября 2016 г
Немного о работе с Rmarkdown прежде чем перейти к делу.
Возможно, у вас возникнет необходимость или личное желание нарисовать что-либо в Rmarkdown. Для этого можно использовать такие прекрасные tools, как:
Тепеть обратимся к условному математическому ожиданию.
Стоит напомнить, что \(E(X|\mathcal{F})\) — это наилучший прогноз \(X\), если мы различаем события из \(\sigma\)-алгебры, согласно интуитивному определению.
8.1 Задание №1
8.1.1 Условия задачи:
Пусть даны случайные величины \(X\), \(Y\) и вероятности их совместного наступления:
| \((X, Y)\) | \(0\) | \(4\) |
|---|---|---|
| \(1\) | \(a = 0.1\) | \(b = 0.2\) |
| \(2\) | \(c = 0.2\) | \(d = 0.5\) |
и дана \(\sigma\)–алгебра \(\mathcal{F} = \{ \{a\} , \{b, c, d\}, \varnothing, \Omega \}\).
Необходимо найти:
a.1. \(E(X|\mathcal{F})\)
a.2. \(E(Y|\mathcal{F})\)
a.3. \(E(XY|\mathcal{F})\)
\(\mathcal{H} = \sigma(Y)\)
c.1. \(E(X|\mathcal{H})\)
c.2. \(E(Y|\mathcal{H})\)
\(\mathcal{A} = \{ \varnothing, \Omega \}\)
d.1. \(E(X|\mathcal{A})\)
d.2. \(E(Y|\mathcal{A})\)
\(\mathcal{K} = \sigma(X, Y)\)
e.1. \(E(X|\mathcal{K})\)
e.2. \(E(Y|\mathcal{K})\)
8.1.2 Решение:
Для начала приведём таблицу в более удобный для решения вид:
| \(\Omega\) | \(a\) | \(b\) | \(c\) | \(d\) |
|---|---|---|---|---|
| \(X\) | \(1\) | \(1\) | \(2\) | \(2\) |
| \(Y\) | \(0\) | \(4\) | \(0\) | \(4\) |
| \(Pr\) | \(0.1\) | \(0.2\) | \(0.2\) | \(0.5\) |
Освежим в памяти смысл \(E(X|{a})\): это математическое ожидание \(X\), если нам известно, что \(a\) — произошло.
a.1. Распишем \(E(X|\mathcal{F})\) по компонентам.
Исходя из условий, \(X\) примет значение 1, если известно \(a\) (смотрим в таблице на пересечение столбца \(a\) и строки \(X\)). Поэтому \({E(X|{a}) = 1}\).
Заданная \(\sigma\)-алгебра не различает значения \(\{b\}, \{c\}, \{d\}\), только “слипшиеся” вместе — \(\{b, c, d\}\). Посчитаем же \(E(X|\{b, c, d\})\): для этого нам потребуется таблица. Вероятность наступления \(b\) среди событий \(b, c, d\): \(\frac{0.2}{(0.2+0.2+0.5)}\) — это доля наступления \(b\), рассуждая интуитивно. Аналогично для \(c\) и \(d\): \(\frac{0.2}{(0.2+0.2+0.5)}\) и \(\frac{0.5}{(0.2+0.2+0.5)}\), соответсвенно. Таким образом, \(E(X|\{b, c, d\}) = 1\frac{0.2}{(0.2+0.2+0.5)} + 2\frac{0.2}{(0.2+0.2+0.5)} + 2\frac{0.5}{(0.2+0.2+0.5)} = 1\frac{2}{9} + 2\frac{2}{9} + 2\frac{5}{9} = \frac{16}{9}\)
В нашу таблицу можно добавить еще одну строку:
| \(\Omega\) | \(a\) | \(b\) | \(c\) | \(d\) |
|---|---|---|---|---|
| \(X\) | \(1\) | \(1\) | \(2\) | \(2\) |
| \(Y\) | \(0\) | \(4\) | \(0\) | \(4\) |
| \(Pr\) | \(0.1\) | \(0.2\) | \(0.2\) | \(0.5\) |
| **$E(X | )$** | \(1\) | \(\frac{16}{9}\) | \(\frac{16}{9}\) |
a.2. Аналогичны рассуждения для \(E(Y|\mathcal{F})\), запишем сразу в таблицу:
| \(\Omega\) | \(a\) | \(b\) | \(c\) | \(d\) |
|---|---|---|---|---|
| \(X\) | \(1\) | \(1\) | \(2\) | \(2\) |
| \(Y\) | \(0\) | \(4\) | \(0\) | \(4\) |
| \(Pr\) | \(0.1\) | \(0.2\) | \(0.2\) | \(0.5\) |
| **$E(X | )$** | \(1\) | \(\frac{16}{9}\) | \(\frac{16}{9}\) |
| **$E(Y | )$** | \(0\) | \(\frac{28}{9}\) | \(\frac{28}{9}\) |
a.3. Случай \(E(XY|\mathcal{F})\) разберём более подробно. \(XY\) примет значения \(0, 4, 0, 8\). То есть, вектор \(X = (1, 1, 2, 2)\), вектор \(Y = (0, 4, 0, 4)\), отсюда получаем, что вектор \(XY = (0, 4, 0, 8)\).
| \(\Omega\) | \(a\) | \(b\) | \(c\) | \(d\) |
|---|---|---|---|---|
| \(X\) | \(1\) | \(1\) | \(2\) | \(2\) |
| \(Y\) | \(0\) | \(4\) | \(0\) | \(4\) |
| \(XY\) | \(0\) | \(4\) | \(0\) | \(8\) |
| \(Pr\) | \(0.1\) | \(0.2\) | \(0.2\) | \(0.5\) |
| **$E(X | )$** | \(1\) | \(\frac{16}{9}\) | \(\frac{16}{9}\) |
| **$E(Y | )$** | \(0\) | \(\frac{28}{9}\) | \(\frac{28}{9}\) |
\(E(X|\mathcal{F})\), как мы уже знаем, разбивается на два случая: \(E(X|\{a\})\) и \(E(X|\{b, c, d\})\).
\(E(X|\{a\}) = 0\), так как значению \(a\) в векторе \(XY\) соответсвует \(0\).
\(E(X|\{b, c, d\}) = 4\frac{0.2}{(0.2+0.2+0.5)} + 0\frac{0.2}{(0.2+0.2+0.5)} + 8\frac{0.5}{(0.2+0.2+0.5)} = 4\frac{2}{9} + 0\frac{2}{9} + 8\frac{5}{9} = \frac{48}{9}\).
Таблица, в свою очередь, примет вид:
| \(\Omega\) | \(a\) | \(b\) | \(c\) | \(d\) |
|---|---|---|---|---|
| \(X\) | \(1\) | \(1\) | \(2\) | \(2\) |
| \(Y\) | \(0\) | \(4\) | \(0\) | \(4\) |
| \(XY\) | \(0\) | \(4\) | \(0\) | \(8\) |
| \(Pr\) | \(0.1\) | \(0.2\) | \(0.2\) | \(0.5\) |
| **$E(X | )$** | \(1\) | \(\frac{16}{9}\) | \(\frac{16}{9}\) |
| **$E(Y | )$** | \(0\) | \(\frac{28}{9}\) | \(\frac{28}{9}\) |
| **$E(XY | )$** | \(0\) | \(\frac{48}{9}\) | \(\frac{48}{9}\) |
По сути, на этом разбор данного задания заканчивается. Однако решение остальных пунктов всё же приведено ниже с оговоркой: оно было сверено, но достоверно не проверено.
- \(\mathcal{H} = \sigma(Y) = \{\{a, c\}, \{b, d\}, \varnothing, \Omega \}\).
c.1. \(E(X|\mathcal{H}) = E(X|\{a, c\}) + E(X|\{b, d\})\).
Посчитаем покомпонентно:
\(E(X|\{a, c\}) = 1\frac{0.1}{(0.1+0.2)} + 2\frac{0.2}{(0.1+0.2)} = \frac{5}{3}\)
\(E(X|\{b, d\}) = 1\frac{0.2}{(0.2+0.5)} + 2\frac{0.5}{(0.2+0.5)} = \frac{12}{7}\)
Таблица примет вид:
| \(\Omega\) | \(a\) | \(b\) | \(c\) | \(d\) |
|---|---|---|---|---|
| \(X\) | \(1\) | \(1\) | \(2\) | \(2\) |
| \(Pr\) | \(0.1\) | \(0.2\) | \(0.2\) | \(0.5\) |
| **$E(X | )$** | \(\frac{5}{3}\) | \(\frac{12}{7}\) | \(\frac{5}{3}\) |
c.2. Механизм решения для \(E(Y|\mathcal{H})\) аналогичный. Запишем ответ в таблицу:
| \(\Omega\) | \(a\) | \(b\) | \(c\) | \(d\) |
|---|---|---|---|---|
| \(X\) | \(1\) | \(1\) | \(2\) | \(2\) |
| \(Y\) | \(0\) | \(4\) | \(0\) | \(4\) |
| \(Pr\) | \(0.1\) | \(0.2\) | \(0.2\) | \(0.5\) |
| **$E(X | )$** | \(\frac{5}{3}\) | \(\frac{12}{7}\) | \(\frac{5}{3}\) |
| **$E(Y | )$** | \(0\) | \(4\) | \(0\) |
- \(\mathcal{A} = \{ \varnothing, \Omega \}\)
d.1. \(E(X|\mathcal{A}) =\) так как \(X\) не зависит от \(\mathcal{A} = E(X) = 1(0.1+0.3) + 2(0.2+0.5) = 1.7\)
d.2. \(E(Y|\mathcal{A}) =\) так как \(Y\) не зависит от \(\mathcal{A} = E(Y) = 0(0.1+0.2) + 4(0.2+0.5) = 2.8\)
И наконец…
- \(\mathcal{K} = \sigma(X, Y)\) — все подмножества \(\Omega\).
e.1. \(E(X|\mathcal{K}) = X\), так как \(X\) — измерима относительно \(\mathcal{K}\).
e.2. \(E(Y|\mathcal{K}) = Y\), так как \(Y\) — измерима относительно \(\mathcal{K}\).
Итак, первое задание разобрано полностью. Хочется верить, что лапши на уши навешано не было.
8.2 Задание №2
8.2.1 Условия задачи:
Это задание — продолжение задачи \(2.39\) из задачника. Ниже вкратце изложены условия:
\(\mathcal{S_n}\) — симметричное случайное блуждание, то есть \(\mathcal{S_n} = X_1 + X_2 + ... + X_n\), где \(X_n\) — независимые и одинаково распределённые случайные величины с вероятностью \(P(X_n = 1) = P(X_n = −1) = 0.5\). Пусть \(T\) — время второго локального максимума \(+1\). Определены следующие \(\sigma\)–алгебры: \(\mathcal{F_n} = \sigma(X_1, X_2, ..., X_n)\) и \(\mathcal{F_T}\) — все события \(X_i\), которые могут быть распознаны до момента \(T\).
Необходимо найти:
\(E(X_{T-3}|\mathcal{F}_T)\)
\(E(T|\sigma(T))\)
\(E(X_T|\sigma(T))\)
\(E(S_T|\sigma(T))\)
8.2.2 Решение:
Напомним, что \(\sigma(T)\) — знание момента времени второго локального максимума \(+1\), а \(\mathcal{F_T}\) — все события \(X_i\), которые могут быть распознаны до момента второго локального максимума \(+1\).
- \(E(X_{T-3}|\mathcal{F}_T)\): событие \(X_{T-3}\) — измеримо относительно \(\sigma\)–алгебры \(\mathcal{F}_T\), поэтому \(E(X_{T-3}|\mathcal{F}_T) = X_{T-3}\).
- \(E(T|\sigma(T))\): аналогично с пунктом a. \(T\) — измерима относительно \(\sigma(T)\), поэотму \(E(T|\sigma(T)) = T\).
- \(E(X_T|\sigma(T))\): так как в \(\sigma(T)\) содержится информация о моменте \(T\), который, грубо говоря, означает переход с \(1\) на \(-1\), то \(E(X_T|\sigma(T)) = -1\).
Наглядное изображение:
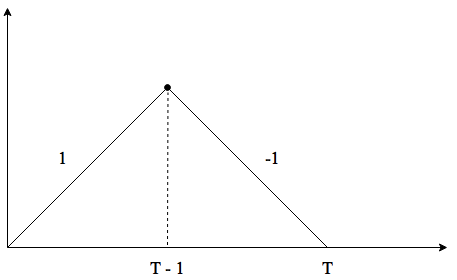
Иллюстрация \(T\) — второго локального максимума \(+1\).
- Не будем создавать интригу и сразу дадим ответ: \(E(S_T|\sigma(T)) = 0\).
Алгоритм решения заключается в кропотливом переборе всех возможных комбинаций \(S_T\) при каждом значении \(T\). Например, при разобранном нами значении \(T=17\) \((S_T|T=17)\) будет принимать значения \(\pm{13}, \pm{11}, \pm{9}, \pm{7}, \pm{5}, \pm{3}, \pm{1}\).
На этом разбор упражнений заканчивается. Как приятный бонус, определим условное математическое ожидание от \(\sigma\)–алгебры формально.
8.3 Определение условного математического ожидания от сигма–алгебры:
Если \(E(|X|) < \infty\), то можно определить \(E(X|\mathcal{F})\).
\(E(X|\mathcal{F})\) — это случайная величина \(\hat{X}\), обладающая следующими свойствами:
1. \(\hat{X}\) измеримо относительно \(\sigma\)–алгебры \(\mathcal{F}\), то есть, зная информацию из \(\mathcal{F}\), можно определить \(X\).
2. \(E(\hat{X}) = E(X)\).
3. Если взять любую \(\mathcal{F}\)–измеримую случайную величину \(Z\), то окажется, что \(cov(Z, X) = cov(Z, \hat{X})\).
Зачастую в задачах данного курса встречается много разных замечательных персонажей, будь то Маша с грибами, Петры с Николаями, злобный Дед Мороз, Дракон с гномами или Виноградная улитка. Для интуитивной интерпретации представленного выше определения, придумаем простого мальчика Васю. Он знает, произошли ли события из \(\mathcal{F}\). Мальчик Вася также может посчитать \(\hat{X}\) (свойство 1), Вася умеет считать \(E(\hat{X})\) и \(E(X)\) (свойство 2), кроме того, мальчик Вася не отличает \(X\) от \(\hat{X}\), если он может считать только ковариации (свойство 3).
Идём дальше.
8.4 Определение геометрий случайных величин:
Для случайных величин, помимо всего прочего, можно определять геометрии. У случайных величин есть длина, а между двумя случайными величинами можно определить угол!
Для решения следующих упражнений, дадим определение двум геометриям:
| \(№\) | \(Г_1\) | \(Г_2\) |
|---|---|---|
| \(dist(X,Y)\) | \(\sqrt{E((X-Y)(X-Y))}\) | \(\sqrt{Var(X-Y)}\) |
| \(cos(X,Y)\) | \(\frac{E(XY)}{dist(0, X)dist(0, Y)}\) | \(\frac{cov(X, Y)}{\sigma_{X}\sigma_{Y}}\) |
| \(<X, Y>\) | \(E(XY)\) | \(Cov(X, Y)\) |
Упражнения же на геометрии случайных величин будут разобраны в следующем конспекте.
8.5 Дружеские рекомендации:
В процессе работы над конспектом часто приходится использовать специальные символы, которые в Rmarkdown записываются достаточно громоздко. Например, за символом \(\mathcal{F}\) скрывается вот такой крокодильчик:
$\mathcal{F}$. Согласитесь, каждый раз набивать руками подобные символы не столь приятно. Гораздо удобнее копировать из заранее созданного файла, в которыйленивыйстудент добавляет специальные символы по мере написания конспекта. И оттуда же берёт уже единожды введёное руками.А вы набивали макет для таблицы самостоятельно? Если ещё нет, то этот генератор таблиц облегчит вашу участь.