Глава 1 Счётные и несчётные множества

Конспект: Людмила Гадий

дата: 2 сентября 2016

Рассмотрим ряд примеров на определение счётности/несчётности множеств:

\(\mathbb{N}\) = {1, 2, 3, …} ;
\(\mathbb{Z}\) = {- … , -3, -2, -1, 0, 1, 2, 3, …} ;
\(\mathbb{Q}\) = { \(\frac{m}{n}\) | \(m\in\mathbb{Z}\), \(n\in\mathbb{N}\)} ;
\(\mathbb{R}\) – множество действительных чисел;
Точки на плоскости с целыми координатами;
[0 ; 1] ;
[0 ; 1]\(\times\)[0 ; 1] = { (x, y) | \(x\in\), \(y\in\) } ;
Множество бесконечных последовательностей из нулей и единиц.

Будет рассматривать эти примеры в ходе изложения в порядке их нумерации.

1.1 Счётное множество

Определение:
Счётное множество - это либо конечное, либо равномощное натуральным числам множество (иными словами, каждому элементу можно сопоставить натуральное число взаимно однозначно, то есть так, что ни один элемент в таких множествах не будет пропущен).

Элементы множества натуральных чисел можно пронумеровать, следовательно множество \(\mathbb{N}\) - счетно.
По определению счетного множества, множество целых чисел \(\mathbb{Z}\) - счётно, так как целые числа можно расположить в виде последовательности 0, 1, −1, 2, −2, 3, −3, … . Иными словами, можно привести взаимнооднозначное соответствие между целыми и натуральными числами, например, таким способом (см. рисунок):
\(0\leftrightarrow1\)
\(1\leftrightarrow2\)
\(-1\leftrightarrow3\)
\(2\leftrightarrow4\)
\(-2\leftrightarrow5\)
\(3\leftrightarrow6\)
…

plot(c(-5:5), c(-5:5), type = 'n', xlab = "", ylab = "", xaxt = "n", yaxt = "n")
axis(1, at = -5:5, labels = -5:5)
axis(2, at = -5:5, labels = -5:5)
x1 <- rep(c(0.5, 0), 3)
r <- seq(1:6) / 2
for (i in 1:6) {
  curve(sqrt((r[i])^2 - (x - x1[i])^2), x1[i] - r[i], x1[i] + r[i], add = TRUE)
  if (i %% 2 == 1) {
    arrows(x1[i] + r[i], 0.01, x1[i] + r[i], 0, length = 0.1)
  } else {
    arrows(x1[i] - r[i], 0.01, x1[i] - r[i], 0, length = 0.1)
  }
}
arrows(-5, 0, 5, 0, col = "blue")
arrows(0, -5, 0, 5, col = "blue")
abline(h = -5:5, v = -5:5, lty = 3, col = "gray")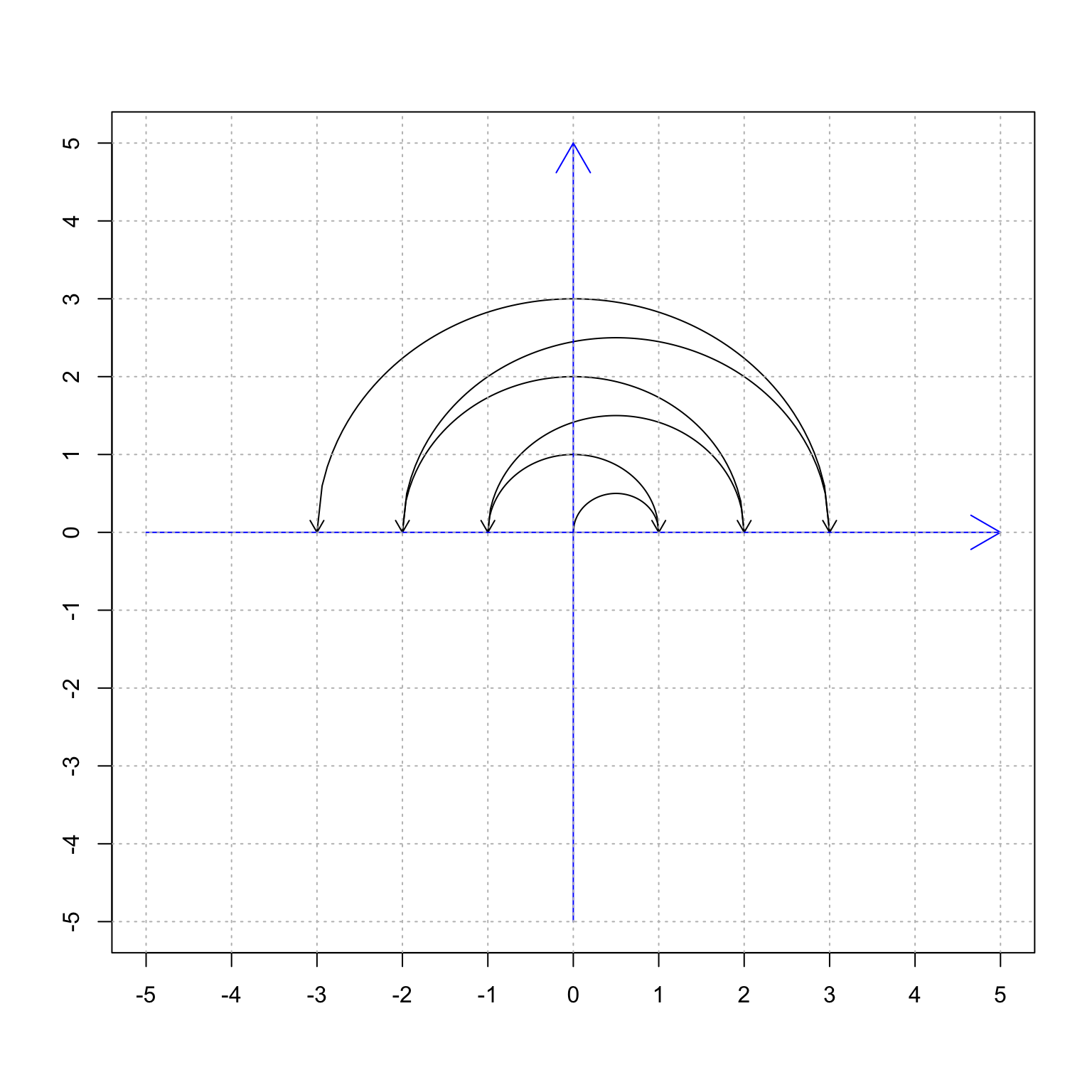

Докажем счетность множества рациональных чисел:
Расположим рациональные числа в виде таблицы, строку которой с номером n образуют дроби со знаменателем n. Нумеруем по прямоугольникам, начиная с нуля и пропуская при этом числа, которые уже получили номер ранее. Так, любое рациональное число получит некоторый номер, что доказывает счетность множества рациональных чисел.

1.2 Сравнимость мощностей

Утверждение: Если множество А равномощно подмножеству В, то либо мощность А меньше мощности В, либо А и В равномощны.

Из курса высшей алгебры:
Для доказательства счетности множества предположим противное. Пусть множество \(\mathbb{R}\) состоит из чисел a₁,a₂,…,a_n,…. Рассмотрим дробные части \(\alpha\)_n чисел a_n, 0 < \(\alpha\)_n < 1, расположим в виде таблицы:
\(\alpha\)₁ = 0, \(\alpha\)₁₁, \(\alpha\)₁₂, …, \(\alpha\)_1n, …
\(\alpha\)₂ = 0, \(\alpha\)₂₁, \(\alpha\)₂₂, …, \(\alpha\)_2n, …
…
Чтобы опровергнуть гипотезу о счетности множества \(\mathbb{R}\), приведем пример числа a, отличного от всех чисел a₁,a₂,…,a_n,… .
Рассмотрим число \(\beta\) = 0, \(\beta\)₁, \(\beta\)₂, …, \(\beta\)_n, … . Пусть \(\beta_1\ne\alpha_{11}\), \(\beta_2\ne\alpha_{22}\), …, \(\beta_n\ne\alpha_{nn}\), тогда \(\beta_k\ne\alpha_k\), k = 1,2,…,n,…, т.е. это число не совпадает ни с одним из чисел a₁,a₂,…,a_n,…, что означает, что наше предположение о том, что все числа множества \(\mathbb{R}\) удалось пронумеровать, привело к противоречию, и множество несчетно.

Кроме того, \(\mathbb{R}\) ~ [0 ; 1] - это несчетные множества с одинаковой мощностью. Однако как можно показать, что \(\mathbb{R}\) не мощнее [0 ; 1] ? Для наглядности можно использовать график арктангенса. Преобразуем его до вида \(atan(x)/pi+1/2\). Видно, что его асимптоты будут иметь координаты 0 и 1 по оси ординат. Также видно, что каждой точке на оси X (эквивалентно множеству \(\mathbb{R}\)) соответствует значение на оси Y, причем каждое из соответствующих значений лежит в промежутке от нуля до единицы. Таким образом, \(\mathbb{R}\) ~ (0 ; 1).

curve(atan(x)/pi + 1/2, from = -10, to = 10, 
      main = "График arctg(x)/pi+1/2", xlab = "x", ylab = "ArcTg(x)") 
abline(v = 0, col = "red")
abline(h = 1, lty = 2, col = "red")
abline(h = 0, lty = 2, col = "red")
abline(h = 0:40/20, v = -20:20/2, lty = 3, col = "gray")
x1 <- tan((1/4 - 1/2)*pi)
arrows(x1, 1/4, 0, 1/4)
arrows(x1, atan(x1)/pi + 1/2, x1, 0)

Проведем в данном случае аналогию с точками на плоскости. Так, например, можно двигаться “по спирали”, пересчитывая тем самым все точки на этой плоскости.
Во избежание путаницы, важно отметить, что в рамках этого способа \((-3,-1)\ne(-6,-2)\), в то время как \(\frac{-3}{-1}=\frac{-6}{-2}\).

plot(c(-5:5), c(-5:5), type = "n", xlab = "", ylab = "")
arrows(-5, 0, 5, 0, length = 0.25, col = "blue")
arrows(0, -5, 0, 5, length = 0.25, col = "blue")
abline(h = -5:5, v = -5:5, lty = 3, col = "gray")
x <- c(0, 1, 1, -1, -1, 2, 2, 1:-2, -2, -2, -2, -2:3)
y <- c(0, 0, 1, 1, -1, -1, 2, 2, 2, 2, 2:-2, -2, -2, -2, -2, -2)
s <- seq(6)
arrows(x[s], y[s], x[s + 1], y[s + 1], length = 0.15, angle = 20)
s <- seq(14) + 7
points(x[s], y[s], pch = 16)

Отрезок [0,1] равномощен множеству всех бесконечных последовательностей нулей и единиц, то есть является несчетным множеством. Подробнее см. в учебнике Н.К.Верещагина и А.Шень Начала теории множеств.
[0 ; 1]\(\times\)[0 ; 1] - декартов квадрат; он обладает большей мощностью, чем отрезок [0 ; 1], который является несчетным множеством. Заключаем, что [0 ; 1]\(\times\)[0 ; 1] - несчетное множество.
Пусть есть некоторое множество А, состоящее из последовательностей 0 и 1. Рассмотрим такие последовательности и пронумеруем их:
\(1\leftrightarrow{\underline{0} ,1,0,1,0,1,0,1,... }\in A\)
\(2\leftrightarrow{0,\underline{0},0,1,0,0,0,1,... }\in A\)
…
Во множестве А содержится бесконечное количество элементов - последовательностей из 0 и 1.

1.3 Доказательство от принцессы

Утверждение: А - несчетно.
Доказательство от принцессы: Тому, кто приведет взаимнооднозначное соответствие между множеством А и множеством натуральных чисел \(\mathbb{N}\), полагается сердце и полцарства в придачу!
Пусть пришел индийский принц. Принц развернул длинный список, и она видит, что он пронумеровал бесконечно много последовательностей из нулей и единиц. Что будет делать принцесса? Предположим, что в его списке, помимо отмеченных нами последовательностей №1 и №2, присутствуют и такие последовательности:
\(3\leftrightarrow{1,1,\underline{1} ,1,1,1,1,1,... }\in A\)
\(4\leftrightarrow{0,0,0,\underline{0},0,0,0,0,... }\in A\).
Чтобы принцу ничего не досталось, принцесса меняет значение i-го элемента i-го списка на противоположное (0 на 1 и 1 на 0 соответственно). Это можно сделать в каждой последовательности, тогда
…
\(101\leftrightarrow{... \underline{1}}\in A\)
…
И такая измененная последовательность не может быть у него ни под каким номером.
Пусть пришел и арабский принц. Принцесса проводит аналогичную операцию по замене значения i-го элемента i-го списка на противоположное:
\(1\leftrightarrow{\underline{1} ,1,1,1,1,1,1,1,1,1,...}\in A\)
\(2\leftrightarrow{1,\underline{0},1,0,0,1,0,0,0,1,...}\in A\)
\(3\leftrightarrow{...\underline{ }...}\in A\)
Аналогичный результат и со списком второго принца. Таким образом, мы можем сделать вывод, что такого взаимнооднозначного соответствия не существует, и принцесса может отказать любому принцу! Отсюда следует, что множество А не равномощно множеству \(\mathbb{N}\).
Пояснение: A > \(\mathbb{N}\) :
\(1\leftrightarrow{100000...}\in A\)
\(2\leftrightarrow{010000...}\in A\)
\(3\leftrightarrow{001000...}\in A\)
\(4\leftrightarrow{000100...}\in A\)
…

1.4 Мораль

Счетные множества - это конечные + равномощные множеству \(\mathbb{N}\) ( \(\mathbb{N}\) , \(\mathbb{Q}\) , \(\mathbb{Z}\times\mathbb{Z}\) ) ;
Несчетная мощность > Счетная мощность : \(\mathbb{R}\) , [0 ; 1] , ( 0 ; 1 ) , [0 ; 1]\(\times\)[0 ; 1] ;
Бесконечности бывают разные: одна больше, другая меньше…
card \(\mathbb{N}\) < card \(\mathbb{R}\) < card { Все подмножества прямой } < …
\(\Uparrow\)
Это самая маленькая бесконечность - она является счетным множеством.
card ~ cardinality